Реферат: Финансовая рента
Тогда
= 
= 
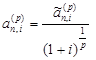. (20)
где 
- эквивалентная учетная ставка.
Из (19), (20) получаем
, (21)
где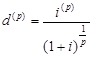 
- эквивалентная номинальная учетная ставка.
Каждое выражение в этом равенстве - современная стоимость процентов, выплачиваемых по займу 1 д. е. на протяжении n лет в соответствии с различными способами выплаты процентов.
Аналогичные соотношения можно получить и для коэффициентов наращения рент.
Если полагают, что срок ренты n = ∞, то ренту называют вечной. Наращенная сумма вечной ренты бесконечна. Однако современную величину такой ренты можно найти.
Для обычной вечной p - срочной ренты с начислением процентов 1 раз в год получаем при n → ∞:
.
Для такой же ренты пренумерандо:
.
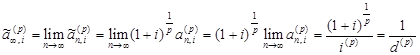Кроме того,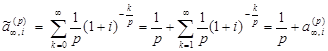 
.
Таким образом, 
, 
, 
. (21)
Если вечная рента является годовой (p = 1), то имеем:
, 
, 
. (22)
Если начало ренты, т.е. начало ее первого периода, переносится в будущее на t единиц времени относительно текущего момента t = 0, то такую ренту называют отсроченной. Современная стоимость отсроченной ренты At определяется следующим образом. Согласно определению современной стоимости потока платежей,
,
где 
, 
, 
- дисконтные множители k - го платежа на временных отрезках [0, tk ], [t , tk ], [0, t ] соответственно. Так как 
, то A - стоимость ренты, рассчитанная на момент начала ее первого периода, т.е. на момент начала неотсроченной ренты.
Следовательно, A - это современная стоимость неотсроченной ренты.
Таким образом, современная стоимость отсроченной ренты определяется путем дисконтирования по процентной ставке ренты в течение времени t современной стоимости A неотсроченной ренты:
, (23)
Рассмотрим зависимость коэффициентов наращения ренты от срока ренты и процентной ставки.
Поскольку характер зависимости не должен зависеть от числа платежей в году, рассмотрим годовую обычную ренту с начислением процентов 1 раз в год.
Имеем 
, 
.
Ситуацию можно рассматривать как беспроцентный долг, выданный в сумме n и возвращаемый равными долями в течение n лет.
Установим зависимость от i коэффициента наращения ренты 
.
.