Реферат: Фізика атомів і молекул

План

1. Використання рівняння Шредінгера до атома водню. Хвильова функція. Квантові числа.

2. Енергія атома водню і його спектр. Виродження рівнів. Правила відбору.

3. Механічний і магнітний моменти атома водню.

1. Використання рівняння Шредінгера до атома водню. Хвильова

функція. Квантові числа

Теорія Бора будови й властивостей енергетичних рівнів електронів у водневоподібних системах знайшла своє підтвердження у квантовій механіці. Квантова механіка також стверджує, що:

a) електрони в атомах водню знаходяться лише в дискретних енергетичних станах. При переході електронів з одних станів в інші випромінюється або поглинається фотон;

б) не існує певних колових орбіт електронів. В силу хвильової природи електрони «розмиті» в просторі подібно до хмарки негативного заряду. Розміри й форму такої хмарки в заданому стані можна розрахувати.

Розглянемо рух електрона в кулонівському полі ядра із зарядом Ze , потенціальна енергія якого виражається формулою

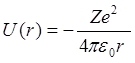, (1)

де r – відстань між електроном і ядром.

Стан електрона в атомі водню або водневоподібному атомі описується деякою хвильовою функцією  , яка задовольняє стаціонарне рівняння Шредінгера:

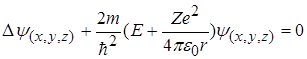, (2)

де 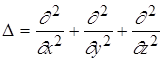― оператор Лапласа; Е ― значення повної енергії електрона в атомі; m ― маса частинки; _(x,y,z) ― хвильова функція у декартовій системі координат.

Для розв’язування рівняння Шредінгера (2), тобто знаходження виду хвильової функції для електрона в атомі водню слід перейти від декартових координат до сферичних. У цьому випадку зв’язок між параметрами цих систем координат визначається з рис. 1.12.

Співвідношення, які пов’язують координати x,y,z декартової прямокутної системи координат із сферичними координатами r, ,  такі:

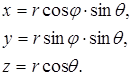(3)

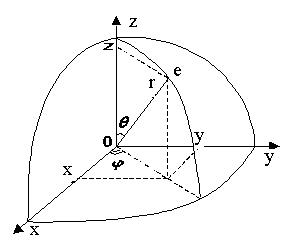
Рис. 1.

Таким чином можна вважати, що хвильова функція  електрона в атомі водню залежить від сферичних координат, тобто  r ,   .

Опустивши досить громіздкі перетворення переходу від декартової системи координат до сферичної, одержимо:

. (4)

Якщо розглядати основний (не збуджений) стан атома водню, то другою й третьою складовими в лівій частині рівняння (4) можна знехтувати. Електрон в такому стані рухається лише по коловій траєкторії і хвильова функція не залежить від  і  . Тому

. (5)

Хвильова функція  електрона в основному стані (5) є функцією лише r , тобто  r ). Такий стан називається s-станом; він має сферично-симетричний характер. Імовірність виявити електрон у заданій точці атома залежатиме лише від r . Умовам стаціонарного стану відповідає центральносиметрична функція, що легко диференціюється і має вигляд:

, (6)

де a ─ деяка стала величина, яка має розмірність довжини.

Необхідні похідні від (6) підставимо в (5). Після скорочення на одержимо:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--