Реферат: Функция многих переменных
знаменатель которой уже разложен на линейные и квадратичные множители. Тогда эту дробь можно разложить на сумму элементарных дробей по таким правилам:
1) множителю (х-а )k соответствует сумма дробей вида
+
+…+
;
2) множителю (x 2 + px + q )I соответствует сумма дробей вида
+
+…+
,
где А 
,М ,N - неопределённые коэффициенты.
Искать эти неопределённые коэффициенты можно исходя из того, что равные многочлены имеют равные коэффициенты при одинаковых степенях х.
Пример. Вычислить интеграл
.
Решение.
+
,
х+ 5=А (х+2 )+В (х+ 1),
А= 4, В =-3.
= 4
-3
= 4ln
-3ln
+C .
3. 1.Интегралы вида
где R (х , у ) – рациональная функция относительно х и у , 
, сводятся к интегралам от рациональных функций с помощью подстановки
ax + b = t
.
2. Интегралы вида
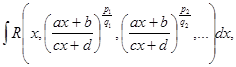
где R – рациональная функция, p , q - целые числа, сводятся к интегралам от рациональных функций с помощью подстановки
= t ,
где п – общий знаменатель дробей 
,
,… .
3. Интегралы вида
(6.1)
всегда сводятся к интегралам от рациональных функций с помощью, так называемой, универсальной тригонометрической подстановки
, 
, 
,
х= 2arctgt , dx = 
.
Замечание. Универсальная тригонометрическая подстановка всегда приводит к цели, но в силу своей универсальности она часто требует неоправданно громоздких вычислений. Поэтому во многих случаях удобнее пользоваться другими подстановками. Рассмотрим некоторые из них.
1) Если в интеграле (6.1) R (-sinx , cosx )= - R (sinx , cosx ), то удобно делать подстановку cosx = t .
2) Если R (sinx ,-cosx )= - R (sinx , cosx ), то удобно делать подстановку sinx = t .
3) Если R (-sinx , -cosx )= R (sinx , cosx ), то удобно делать подстановку
tgx = t , 
, 
,
х = arctgt , dx= 
.
4. Рассмотрим более детально интегралы вида
,
где т , п – целые числа.
1) Если т – нечётное положительное число, то удобно делать подстановку cosx = t .
2) Если п – нечётное положительное число, то удобно делать подстановку sinx = t .
3) Если оба показателя т и п – чётные неотрицательные числа, то надо делать понижение степени синуса и косинуса по формулам
, 
.
4) Для нахождения интегралов вида
, 
удобно пользоваться формулами
