Реферат: функция
2. Область значения степенной функции – множество всех положительных чисел.
3. Степенная функция непериодична, не является четной и не является нечетной.
4. Степенная функция непрерывна во всей области определения.
5. Степенная функция дифференцируема во всей области определения, и ее производная вычисляется по формуле
( x a ) ¢ = a . x a -1 .
Степенная функция x a монотонно возрастает во всей области определения при a <0.
6.
 |  |
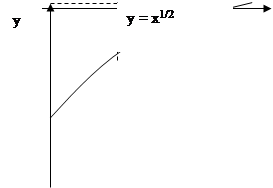
0 1 x 0 1 x
7. При a <0 и a >1 график степенной функции направлен вогнутостью вверх, а при 0<a <1 – вогнутостью вниз.
Показательная функция (экспонента).
Это функция вида 
(
, 
). Для неё 
, 
, 
, и при 
график имеет такой вид:
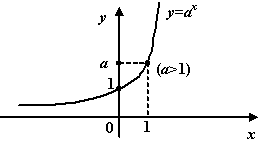
.График показательной функции при
При 
вид графика такой:
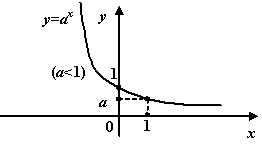
Рис.1.20.График показательной функции при
1. Число 
называется основанием показательной функции. Область определения функции – вся числовая прямая.
2. Область значения функции – множество всех положительных чисел.
3. Функция непрерывна и дифференцируема во всей области определения. Производная показательной функции вычисляется по формуле
(a x )¢ =a x lna
4. При а >1 функция монотонно возрастает, при а <1 монотонно убывает.
5. Показательная функция имеет обратную функцию, называемую логарифмической функцией.
6. График любой показательной функции пересекает ось 0y в точке y =1.
7. График показательной функции – кривая, направленная вогнутостью вверх.
Логарифмическа я функция .
Это функция вида 
(, ). Для неё 
, 
, 
, и при график имеет такой вид:
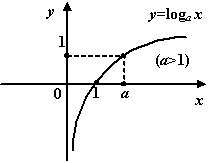
График логарифмической функции при
При график получается такой:
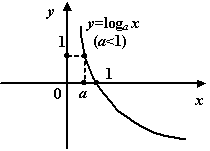
График логарифмической функции при
1. Число называется основанием логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия. Область определения логарифмической функции – промежуток (0; +¥).
2. Область значения логарифмической функции – вся числовая прчмая.
3. Логарифмическая функция непрерывна и дифференцируема во всей области определения. Производная логарифмической функции вычисляется по формуле
( loga x) ¢ = 1/(x ln a).
4. Логарифмическая функция монотонно возрастает, если а >1. При 0<a <1 логарифмическая функция с основанием а монотонно убывает.
5. При любом основании a >0, a ¹1, имеют место равенства
loga 1 = 0, loga a =1.
6. При а >1 график логарифмической функции – кривая, направленная вогнутостью вниз; при 0<a <1 – кривая, направленная вогнутостью вверх.
тригонометрические функции
Функции sin a , cos a , tg a , ctg a называются тригонометрическими функциями угла a. Кроме основных тригонометрических функций sina, cosa, tga, ctga.
Функция синус
.
. Для неё ; функция периодична с периодом 
и нечётна. Её график таков:
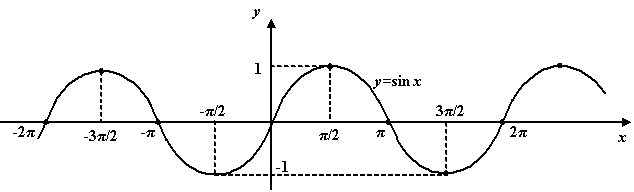
График функции 
 |  |
Синусом числа х называется число, равное синусу угла в радианах.