Реферат: функция
4.Функция tg х – периодическая. Наименьший положительный период функции равен p:
tg (х+p)= tg х.
5.Нули функции: tg х=0 при x=pn, n ÎZ .
6.Промежутки знакопостоянства:
tg х>0 при xÎ (pn ; (p/2)+pn ), n ÎZ ,
tg х<0 при xÎ ((-p/2)+pn ; pn ), n ÎZ .
7.Функция tg х непрерывна и дифференцируема при любом значении аргумента из области определения:
(tg х)¢ =1/cos2 x.
8.Функция tg х возрастает в каждом из промежутков ((-p/2)+pn; (p/2)+pn ), n ÎZ ,
Функция котангенс.
![]() (в англоязычной литературе также
(в англоязычной литературе также ![]() ). По определению,
). По определению, ![]() . Если
. Если 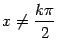 (
( ![]() ), то
), то  . Функция
. Функция ![]() нечётна и периодична с периодом
нечётна и периодична с периодом ![]() ;
;
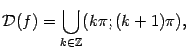
то есть ![]() не может принимать значения вида
не может принимать значения вида ![]() ,
, ![]() , при которых
, при которых ![]() обращается в 0.
обращается в 0.
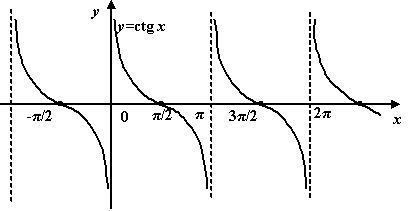
1.График функции ![]() Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn , n ÎZ .
Область определения функции – множество всех действительных чисел, кроме чисел вида х=pn , n ÎZ .
2.Область значения – множество всех действительных чисел.
3.Функциясtg х – нечетная: сtg (-х)=- сtg х.
4.Функция сtg х – периодическая. Наименьший положительный период функции равен p:
сtg (х+p)= ctg х.
5.Нули функции: ctg х=0 при x=(p/2)+pn, n ÎZ .
6.Промежутки знакопостоянства:
ctg х>0 при xÎ (pn ; (p/2)+pn ), n ÎZ ,
ctg х<0 при xÎ ((p/2)+pn ; p(n +1)), n ÎZ .
7.Функция ctg х непрерывна и дифференцируема при любом значении аргумента из области определения:
(ctg х)¢ =-(1/sin2 x).
8.Функция ctg х убывает в каждом из промежутков (pn; p(n +1)), n ÎZ .
Обратные тригонометрические функции.
Это функции арксинус, арккосинус, арктангенс и арккотангенс. Они определяются как функции, обратные к главным ветвям синуса, косинуса, тангенса и котангенса соответственно.
Arcsin x :
1. Область определения – [-1; 1].
2. Область значений – [-П\2; п\2].
3. Монотонно возрастающая функция. (рис. 12)
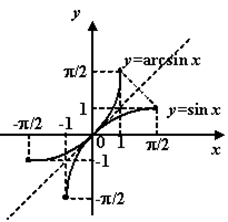
Графики главной ветви ![]() и
и ![]()
Arctg x :
1. Область определений – R.
2. Область значений - интервал (-П\2; П\2).
3. Монотонно возрастающая функция.
4. прямые у=-П\2 и у=П\2 – горизонтальные асимптоты.(рис. 13)
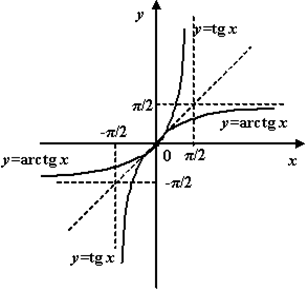
Графики главной ветви ![]() и
и ![]()
Список использованной литературы