Реферат: функция

2. Область значения – промежуток [-1; 1].

3. Функцияsin х – нечетная: sin (-х)=- sin х.

4. Функция sin х – периодическая. Наименьший положительный период равен 2p:

sin (х+2p)= sin х.

5. Нули функции: sin х=0 при x=pn, n ÎZ .

6. Промежутки знакопостоянства:

sin х>0 при xÎ (2pn ; p+2pn ), n ÎZ ,

sin х<0 при xÎ (p+2pn ; 2p+2pn ), n ÎZ .

7. Функция sin х непрерывна и имеет производную при любом значении аргумента:

(sin х)¢ =cos x.

8. Функция sin х возрастает при xÎ ((-p/2)+2pn; (p/2)+2pn ), n ÎZ ,

и убывает при xÎ ((p/2)+2pn ; ((3p)/2)+ 2pn ), n ÎZ .

9. Функция sin х имеет минимальные значения, равные –1, при х=(-p/2)+2pn , n ÎZ , и максимальные значения, равные 1, при х=(p/2)+2pn , n ÎZ .

Функция косинус.

. Эта функция связана с синусом формулой приведения: ; ; период функции равен ; функция чётна. Её график таков:

1.График функции Область определения – множество всех действительных чисел.

2.Область значения – промежуток [-1; 1].

3.Функцияcos х – четная: cos (-х)=cos х.

4.Функция cos х – периодическая. Наименьший положительный период равен 2p:

cos (х+2p)= cos х.

5.Нули функции: cosх=0 при x=(p/2)+2pn, n ÎZ .

6.Промежутки знакопостоянства:

cos х>0 при xÎ ((-p/2)+2pn; (p/2)+2pn )), n ÎZ ,

cos х<0 при xÎ ((p/2)+2pn ); ((3p)/2)+ 2pn )), n ÎZ .

7.Функция cos х непрерывна и дифференцируема при любом значении аргумента:

(cos х)¢ =-sin x.

8.Функция cos х возрастает при xÎ (-p+2pn; 2pn ), n ÎZ ,

и убывает при xÎ (2pn ; p+ 2pn ), n ÎZ .

Функция cos х имеет минимальные значения, равные –1, при х=p+2pn , n ÎZ , и максимальные

Функция тангенс.

(в англоязычной литературе обозначается также ). По определению, . Функция нечётна и периодична с периодом ;

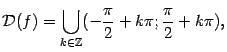
то есть не может принимать значений , , при которых (стоящий в знаменателе) обращается в ноль.

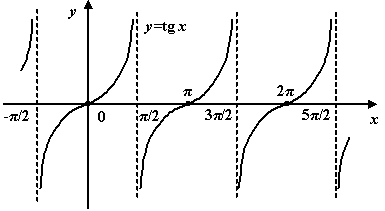
1.График функции Область определения функции – множество всех действительных чисел, кроме числа х=p/2+pn , n ÎZ .

2.Область значения – множество всех действительных чисел.