Реферат: Гидравлика 2

На рис. 3 и 4 показаны вакуумметрические высоты для случаев вакуума в капельной жидкости и газе. Давление измеряется в единицах силы, отнесенных к единице площади. В системе СИ единицей давления служит Н/м² = Па (паскаль), а в технической системе – кгс/см² = ат (техническая атмосфера). Наряду с этими, как следует из (42) и (44), давление можно, измерять в единицах длины столба данной жидкости.

Общей формулой перевода единиц давления в линейные единицы является

. (45)

При выражении давления высотой столба жидкости чаще всею применяют метры водяного столба, миллиметры ртутного столба и миллиметры спиртового столба .

Гидростатический закон распределения давления, выраженный формулой (34), справедлив, очевидно, для любого положения координатной плоскости хОу. Эту плоскость называют плоскостью сравнения, а величину – гидростатическим напором. Величину , где – избыточноедавление, называют пьезометрическим напором. Из формулы (34) следует, что напоры и постоянны для всех точек данной массы покоящейся жидкости.

2. Силы давления жидкости на твердые поверхности

В общем случае воздействие жидкости на твердую поверхность S сводится к сумме элементарных сил , действующих на малых площадках dS , составляющих эту поверхность (рис. 5).

Если – единичный вектор нормали к поверхности S, внешней к объему жидкости, а – давление на площадке dS , то сила .

Суммируя систему сил , получаем выражение для главного вектора

, (46)

называемого силой давления жидкости на поверхность S , и выражение для главного момента

, (47)

где – радиус-вектор площадки относительно центра приведения системы сил.

Рассмотрим несколько частных случаев.

2.1.Равномерное давление на плоскую стенку (р = const ., п= const ).

В этом случае суммируемые векторы составляют систему параллельных и одинаково направленных сил. Такая система всегда может быть сведена только к силе давления . При р = const и n = const из выражения (46) получаем

. (48)

Линия действия силы проходит через центр тяжести площади S.

Равномерное давление может создаваться покоящимся газом, так как благодаря малой его плотности можно пренебречь действием массовых сил и считать давление одинаковым во всех точках газа.

Равномерное давление может создаваться и капельной жидкостью, например, при ее воздействии на горизонтальные площадки, в случае абсолютного покоя или движения сосуда с ускорением вверх или вниз.

Величина силы при равномерном распределении давления не зависит от ориентации плоской стенки S в пространстве и вычисляется по формуле .

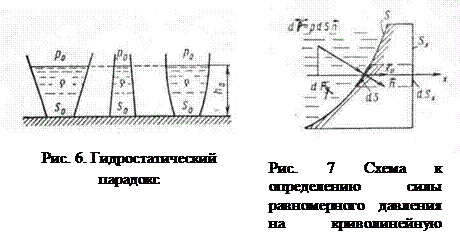
Например, для схемы на рис. 6 давление на дне , а сила . Заметим, что сила давления на дно не зависит от формы сосуда (гидростатический парадокс).

2.2.Сила равномерного давления на криволинейную стенку (, )

В этом случае элементарные силы имеют разные направления. Главный вектор системы вычисляется через свои проекции. Чтобы найти его проекцию на ось х , проектируем на эту ось векторы (рис.7).

,

где – единичный вектор оси x ; – проекция площадки dS на плоскость, нормальную оси х. Искомая величина при

. (49)

Линия действия силы проходит через центр тяжести площади проекции . Таким образом, величина проекции на направлении оси x силы равномерного давления р на криволинейную поверхность S равна произведению давления и площади проекции S_x этой криволинейной поверхности на плоскость. нормальной оси х . Если такие проекции на три взаимно ортогональные оси пересекаются в одной точке, то система сил может быть сведена только к силе давления, величина которой

, (50)

а направление определяется направляющими косинусами