Реферат: Информатика

y₂ =0 когда x=0

y₂ =4 при x=±2

По графику определяем,что уравнение имеет несколько корней. Для уточнения корня выберем интервал [0,1]. Уточняем корень по формуле Ньютона:

x_n+1 = x_n -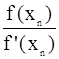

Необходимо выбрать начальное значение x₀ , исходя из условия сходимости:

f(x₀ )f "(x₀ )>0

f(x)= tg(0. 5x+0. 2) – x²

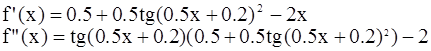
Проверяем условия сходимости для x=0 :

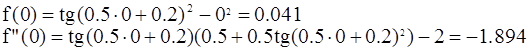
f(0)f"(0)<0,условие не соблюдается

Проверяем условие сходимости для x=1. 0 :

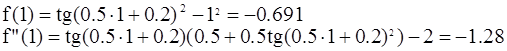
f(0)f"(0)>0,условие соблюдается

берём за x₀ =1

и условие:

Т=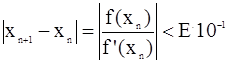

Решение запишем в виде таблицы:

n	x n	f(x n )	f '(x n )		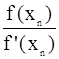T<E 10-1
0	1. 000000	-0. 158000	-1. 151000	0. 137271	Нет
1	0. 862728	-0. 013000	-0. 976000	0. 013119	Нет
2	0. 849416	-0. 000467	-0. 958000	0. 000487	Нет
3	0. 848929	-0. 000009	-0. 958000	0. 000009	Да
4	0. 848920

В результате проделанной работы мы определили один корень уравнения вида tg(0. 5x+0. 2)=x² графически,а затем уточнили его методом Ньютона и получили

X=0. 848929

Вывод по решению:

В результате проделанной работы мы определили один корень уравнения

Tg(0. 5x+0. 2)=x² графически, а затем уточнили его методом Ньютона и получили x=0. 848929

2 . Задача 2

2. 1. Постановка задачи

Выбрать формулу интерполяции и с её помощью определить значение функции в точке x=0,38. Функция задана в виде таблицы 2. 1,Степень интерполяционного многочлена равна 3.

Таблица 2. 1

0,15	0,860708
0,25	0,778801
0,30	0,740818
0,40	0,670320
0,45	0,637628
0,55	0,576950
0,60	0,548812
0,65	0,522046
0,70	0,496585
0,75	0,472237

2. 2. Решение

Решение будем производить методом Лагранжа. Oцениваем шаг

h=x_i+1 -x_i

В этой таблице h=const. Для интерполяции функции с произвольно задаными узлами выбираем интерполяционный многочлен Лагранжа: