Реферат: Интеграл по поверхности первого рода

Любая другая векторная линия проходящая через точки контура проходит либо внутри трубки либо вне трубки.

В случае потока жидкости , векторная трубка -это часть пространства, которую заполняет при своем перемещении объем жидкости.

Интенсивностью векторной трубки называется поток поля через поперечное сечение этой трубки.

3. Если поле соленоидальное в односвязной области , то интенсивность векторной трубки постоянна вдоль всей трубки.

Доказательство:

- боковая поверхность, векторные линии перпендикулярны . Следовательно (нормаль к есть нормаль поля т.е. )

и имеют противоположные направления.

.

Поток через любое поперечное одно и тоже если соленоидальное.

4. В соленоидальном поле векторные линии не могут ни начинаться ни заканчиваться внутри поля. Они либо замкнуты, либо имеют концы на границе поля, либо имеют бесконечные ветви.

Доказательство:

По свойству 3 интенсивность трубки одинакова , хотя поперечное сечение в точке М равно нулю, в т М . Это невозможно т.к. непрерывен в любой точке.

Теорема Стокса.

Вихрь. Ротор.

Циркуляция.

1. Теорема Стокса

.

С понятием циркуляции тесно связано понятие ротора или вихря. Локальной характеристикой поля связанной с завихренностью является ротор.

Плоское поле.

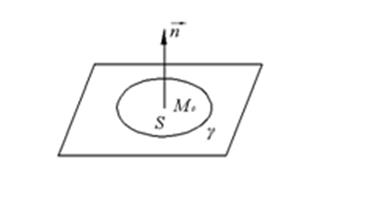
S площадь внутри

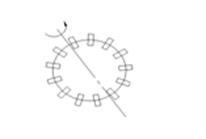
поле скоростей текущей жидкости

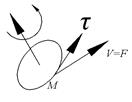
В поле поместим колесо с лопастями, вдоль . Частицы жидкости, действуя на эти лопасти создадут вращательный момент, суммарное действие которых приведут колесо во вращение вокруг своей оси. Вращательное действие поля скоростей жидкости будет в любой точке М характеризовать на касательной к окружности , т.е. скалярное произведение . Суммирование вращательных действии жидкости по всему контуру колесика приведут к понятию циркуляции вектора =

Будет определять угловую скорость вращения колеса, а знак циркуляции покажет в какую сторону вращается колесико относительно выбранного направления.

Циркуляция любого поля определяет его вращательную способность вокруг данного направления и характеризует завихренность поля в этом направлении.