Реферат: Интеграл по поверхности первого рода
. Максимум вихря, если 
- плотность циркуляции 
в точке 
.
Если пространственное поле, то можно говорить о завихренности в направлении 
.
- завихренности в направлении 
.
Определение: 
в точке 
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру 
в плоской области 
, перпендикулярной этому направлению , к величине площади S этой области, когда 
, а область стягивается в точке 
т. е.,
- контур лежащий в плоскости перпендикулярной к вектору
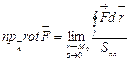
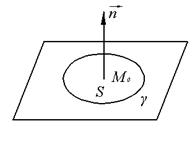
Теорема Стокса. 
-поверхностно-односвязная область. 
- кусочно- гладкий контур в , 
-кусочно-гладкая поверхность натянутая на 
.
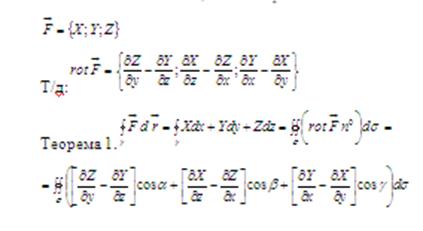
Следовательно циркуляция вектора 
вдоль 
равна потоку 
- вихря 
через 
в направлении
Теорема 2.
В частности
.
Пример. Найти циркуляцию 
по сечению сферы 
плоскостью 
.
Решение.
Потенциальное поле.
Свойства.
Потенциал поля.
Восстановление потенциала U(M) по 
Потенциальное поле.
Определение. Векторное поле 
называется потенциальным в области 
, если существует скалярное поле 
является полем градиента этого скалярного поля 
.
;
.