Реферат: Исследование математических моделей оптимизации обслуживания сложных систем

· E₀ , если в момент t система работоспособна и до отказа проработает время, большее или рав­ное z;

· E₁ , если в момент t система работоспособна и до отказа проработает время, меньшее z;

· E₂ , если в момент t в системе проводится вне­плановый аварийно-профилактический ремой z;

· E₃ , если в момент t в системе проводится преду­предительная профилактика.

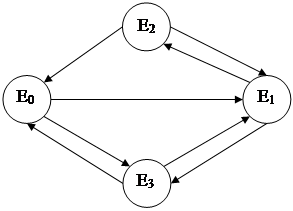
Рисунок 2 – Диаграмма переходов процесса x(t) (Стратегия В)

Определенный случайный процесс является регенерирующим (например, иомен там и регенерации будут моменты переходов в состоянии апериодическим, если предположить, что хотя бы од на из случайных величин время безотказной работы период предупредительны профилактик или у - время восстановления является не­прерывной случайной величиной. Можно утверждать, что при длительной эксплуатации характеристики качества функционирования выражаются дробно-линейным функцио­налом:

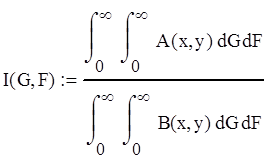(2.2)

Предположим теперь, что функция F(y) известна лишь в отдельных точках, т. е.

F(y) Є Щ(n,y,р). (2.3)

Тогда задача заключается в определении гарантированного среднего выигрыша и функции G*(x), которая определяет периоды профилактики, обеспечивающие этот гарантированный выигрыш,

I(G^* ,F^* ) = max min I(G,F), где G Є Щ, F Є Щ(n,y,р). (2.4)

Гарантированный выигрыш определяется как выигрыш, получаемый при наилучшей функции распределения G*(x) и наихудшей функции распределения F*(y). Ес­ли функционал (2.2) выражает потери, то необходимо брать максимум по F Є Щ(n,y,р) и минимум по G Є Щ.

Расчёт по статистическим данным:

Методика определения минимаксных периодов проведения плановых предупредительных профилактик гарантированных значений показателей качества функционирования:

Исходные данные для расчета :

· вектор y = (y₀ =0,y₁ ,y₂ ,…,y_n ) и вектор р = (р₀ =0, р₁ , р₂ ,…, р_n );

· средняя длительность плановой предупредительной профилактики Т_pp ;

· средняя длительность внепланового аварийно-профилактического ремонта Т_ap ;

· потери за единицу времени при проведении плановой предупредительной профилактики С_pp ;

· потери за единицу времени при проведении внепланового аварийно-профилактического ремонта С_ap ;

· прибыль C0 , получаемая за единицу времени безотказной работы системы;

· оперативное время Z работы системы, необходимое для выполнения задачи.

Формулы для расчёта минимаксных периодов профилактик и гарантированных значений показателей качества функционирования:

· Коэффициент готовности.Определяется номер k₀ при котором достигает максимума выражение

, (2.5)

где k = 0,1,2,..., n.

Если максимум A_k достигается при k₀ <n, то плановые предупредительные профилактики следует проводить в момент ф₀ = y_{k 0+1} -0. Если k₀ = n, то ф₀ = ∞, т.е. плановые предупредительные профилактики прово­дить нецелесообразно.

· Вероятность выполнения задачи.

Определяется номер k₀ (0 ≤ k₀ ≤ n), для которого y_{k 0} – z ≤ 0, y_{k 0+1} – z > 0.

Определяется максимальное значение отношения выражений (1.6) к (1.7).