Реферат: Исследование предельных процессов для числовых последовательностей с применением графических калькуляторов
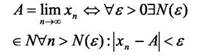
Исходя из постановки задачи определения минимального номера N()ε по
заданному ε, начиная с которого выполняется неравенство:
![]()
рассмотрим функцию f (n ):
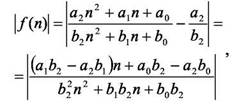
(экстраполируя f на положительную полуось R+)
От рассмотрения функции f(n)
перейдем к рассмотрению функции f (n ), так как график функции f()n отличается от графика функции f()n (в смысле выявления точек экстремума, точек несуществования производной) только появлением дополнительных угловых точек графика на оси абсцисс.
Как же ведет себя функция f(n)?
Во-первых, она может иметь точки раз-
* * рыва n1* и n*2:
![]()
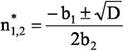
Если же D < 0, то f непрерывна на
R+
Во-вторых, она имеет точки экстремума, для определения которых необходимо решить уравнение: f(nj = 0 и выявить характер критических точек.
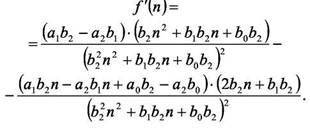
От рассмотрения уравнения f (n ) = 0 перейдем к рассмотрению уравнения:
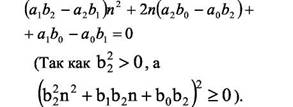
Вычислим критические точки n1 и n2 функции f(n): Если a1b2 − a2b1 ≠ 0, то, учитывая
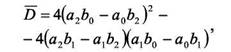
получим: Если D≥0,то
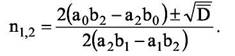
Если D < 0, то действительных критических точек нет. Если же a2b1 − a1b2 = 0, то
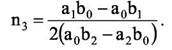
Нахождение угловых точек осуществляется в результате анализа функции
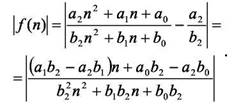
Угловые точки означают пересечение графика данной функции с осью абсцисс, то есть точки, где график функции резко меняет направление, поскольку данная функция является зеркальным отображением функции f ()n j (то есть отрицательные области графика зеркально отображаются относительно оси абсцисс).