Реферат: Исследование предельных процессов для числовых последовательностей с применением графических калькуляторов

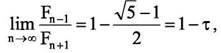
то есть при достаточно больших n (больше 10) точки разбиения методом Фибоначчи и золотого сечения практически совпадают. Это означает, что в данном случае метод Фибоначчи и метод золотого сечения по своей эффективности одинаковы, что и было подтверждено практическими испытаниями.

Метод дихотомии (бисекции)

Метод дихотомии состоит в разбиении интервала [a;b] точкой x пополам. Алгоритм метода дихотомии аналогичен алгоритму метода золотого сечения. Метод дихотомии является менее эффективным в данном случае, чем методы золотого сечения и Фибоначчи.

Описание лабораторной работы

Лабораторная работа по нахождению минимального номера N()ε может быть разделена на три этапа: I этап "Творческий поиск"

Студентам индивидуально-аналитическим методом оценок предлагается найти номер n0, начиная с которого выполняется xn − A < ε (например, ε = 0,05). Ввиду индивидуальности задания и различия способов оценки неравенства пути поиска решения проблемы могут быть весьма различными. IIэтап "Соревнование"

Данный этап подразумевает отыскание более точного значения номера n0 с аналогичными условиями выполнения. Студенты разделяются на m групп по 3 -4 человека, находят оптимальный общий метод оценки, благодаря чему вносится элемент соревнования, основанный на нахождении каждой из групп более точной оценки.

Преподаватель фиксирует найденные в группах номера nk (k = 1, 2, ….. , m) и оценивает правильность и эффективность оценочных процедур. /// этап "Нахождение минимального номера N()ε"

Данный этап является заключительным, поскольку именно здесь студенты получают возможность вычислить минимальный номер N(ε), начиная с которого выполняется неравенство

Предлагаются два возможных пути решения данной задачи: - Последовательное снижение по номерам вниз до тех пор, пока выполняется

< ε (что является трудоемким процессом и неэффективным);

- Использование одного из численных методов (золотого сечения, Фибоначчи или метод дихотомии (бисекции));

- Использование метода случайного поиска.

Ниже представлено описание соответствующей программы для нахождения N(ε) при ε = 0,05 и n0 =10000 для последовательности

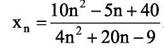
Описание программы

Итак, перейдем непосредственно к программе "NUMBERS", реализующей следующие задачи:

1. Определение минимального номера N(ε) по заданным коэффициентам последовательности a0, a1, a2, b0, b1, b2 и ε.

2. Отслеживание на графике характера функции f(n), определение ее точек разрыва, экстремума и угловой точки, интервалов возрастания и убывания.

Сначала необходимо из окна главного меню войти в режим программирования (PRGM), находящийся под восьмым номером, при помощи активации соответствующей пиктограммы нажатием клавиши "EXE" (рис. 3,a). Затем из представленного списка выбрать программу с именем "NUMBERS"и активизировать ее аналогичным способом (рис. 3,b). Началом работы программы является окно приветствия с полным названием программы "PROGRAM MIN N(E) OF

SQRT POSL" (программа определения номера N()ε, рис. 3,c). Очередное нажатие клавиши "EXE" открывает диалоговое окно для последовательного ввода значений коэффициентов последовательности a0, a1, a2, b0, b1, b2, а также ε и n0.

После ввода значений вышеуказанных параметров последующее нажатие клавиши "EXE" приводит к появлению меню со следующими составляющими (рис. 3,d):

- CONTINUING CALC (1) - подтверждение выполнения последующих вычислительных операций;

- RELOAD FUNCT (2) - только перезагрузка коэффициентов последовательности a0, a1, a2, b0, b1, b2;

- RELOAD LIMIT (3) - только перезагрузка значений ε и n0;

- RELOAD ALL (4) - перезагрузка коэффициентов последовательности a0, a1, a2, b0, b1, b2 и значений ε и n0;

- EXIT (5) - выход из программы.

После очевидного выбора продолжения расчетов путем ввода цифры "1" и нажатия клавиши "EXE" мы попадаем в следующее меню с ниже перечисленными составляющими (рис. 3, e):