Реферат: Исследование предельных процессов для числовых последовательностей с применением графических калькуляторов

чие либо одной такой точки, либо вовсе ее отсутствие.

Откуда

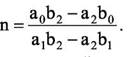
Итак, когда найдены B1 и B2 - точки разрыва, и E1, E2 - точки экстремума f()n и угловая точка G для функции

f ()n, определим интервал [nx;n0], на котором следует искать минимальный N()ε:

nx =max{B1,B2,E1,E2,G},

n0 - теоретически найденный номер аналитическим методом.

Теперь непосредственно рассмотрим вычислительные процедуры для нахождения N()ε, то есть три численных метода, которые применялись для вычисления минимального номера N(ε) при разработке программы "NUMBERS".

Метод золотого сечения

Золотое сечение, открытое Евклидом, состоит в разбиении интервала [а; b] точкой x на две части таким образом, чтобы отношение длины всего интервала к большей части было равно отношению большей части к меньшей:

Золотое сечение производят две точки:

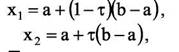
где

(в качестве точки x будем

брать точку х1).

Алгоритм метода золотого сечения для интервала []nx;n0 J следующий:

1. Вычислить значение x.

2. Вычислить значение f()x.

3. Если f(x)< ε, то для дальнейшего деления оставляют интервал [nx;x].

4. Если f(x)≥ ε, то для дальнейшего деления оставляют интервал [x;n0].

Процесс деления продолжают до тех пор, пока длина интервала неопределенности не станет равной 1, то есть точки nx и n0 станут соседними. Искомым N(ε) будет номер n0.

При написании программы использованы стандартные функции: int - получение целой части числа, frac - получение дробной части числа.

Метод Фибоначчи

Как известно, числа Фибоначчи определяются соотношениями:

Используя числа Fn, строим n-точечный последовательный метод, который принято называть методом Фибоначчи. Как и метод золотого сечения, метод Фибоначчи состоит в задании на интервале [a;b] точки х1 или симметричной ей точки х2:

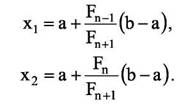
В качестве x - точки разбиения интервала будем брать точку хь Алгоритм метода Фибоначчи совпадает с алгоритмом метода золотого сечения. Единственный недостаток метода Фибоначчи в том, что нужно заранее задать количество проходов.