Реферат: Классический метод. Постоянное напряжение источника

Дано: E = 150В; E_m = 150В; w = 7000 рад/с; y_e = 120°; L = 4 мГн; C = 5 мкФ; R ₁ = 6 Ом; R ₂ = 10 Ом; R ₃ = 5 Ом; R ₄ = 4 Ом.

Найти: u_C (t ).

Классический метод. Постоянное напряжение источника.

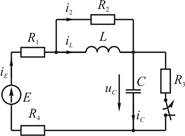Сопротивление последовательного соединения R ₁ , R ₄

R ₁₄ = R ₁ + R ₄ = 6 + 4 = 10 Ом.

Алгебраизованное выражение для входного комплексного сопротивления относительно источника

Z (p ) = + + R ₁₄ = .

Характеристическое уравнение Z (p ) = 0,

R ₃ (R ₂ + R ₁₄ )LC p ² + ((R ₂ + R ₃ + R ₁₄ )L + R ₂ R ₃ R ₁₄ C )p + R ₂ (R ₃ + R ₁₄ ) = 0;

5∙(10 + 10)∙4∙10^-3 ∙5∙10^-6 p ² + ((10 + 5 + 10)∙4∙10^-3 + 10∙5∙10∙5∙10^-6 )p + 10∙(5 + 10) = 0:

Корни характеристического уравнения p ₁ = – 1510 с; p ₂ = – 49700 с.

Свободная составляющая тока в индуктивности i_{L св} = A ₁ e ^{p 1 t} + A ₂ e ^{p 2 t} = A ₁ e ^{–1510 t} + A ₂ e ^{–49700 t} .

Схема до коммутации.

Начальное значение тока в ветви c индуктивностью i_L (0) = E /(R ₁₄ + R ₃ ) = 150/(10 + 5) = 10 А.

Начальное значение напряжения на емкости u_C (0) = i_L (0)R ₃ = 10∙5 = 50 В.

Схема после коммутации.

Принужденная составляющая напряжения на емкостиu_{C пр} = E = 150 В.

Переходное напряжение на емкости и его производная по времени

u_C (t ) = u_{C пр} + u_{C св} (t ) = 150 + A ₁ e ^–1510t + A ₂ e ^–49700t ;

= – 1510A ₁ e ^–1510t – 49700A ₂ e ^–49700t .

Система уравнений для определения неизвестных коэффициентов

u_C (0) = u_{C пр} (0) + u_{C св} (0) = 150 + A ₁ + A ₂ ;

= – 1510A ₁ – 49700A ₂ .

Уравнения по закону Кирхгофа для схемы после коммутации при t = 0

для правого узла – i_C (0) + i_L (0) + i ₂ (0) = 0;

для левого контура R ₁₄ i_E (0) + L – u_C (0) = E ;

для верхнего контура R ₂ i ₂ (0) – L = 0.

Исключение величин i ₂ (0), : (R ₁₄ + R ₂ )i_C (0) – R ₂ i_L (0) – u_C (0) = E ;

(10 + 10)∙i_C (0) – 10∙1,47 – 30,0 = 150;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--