Реферат: Кривизна плоской кривой Эволюта и эвольвента
Найдём выражение дифференциала дуги.
 Пусть имеется на плоскости кривая, заданная уравнением y=f(x). Пусть M0(x0, y0)- некотрая фиксированная точка кривой. Обозначим через s длину дуги M0M (рис.
Пусть имеется на плоскости кривая, заданная уравнением y=f(x). Пусть M0(x0, y0)- некотрая фиксированная точка кривой. Обозначим через s длину дуги M0M (рис.
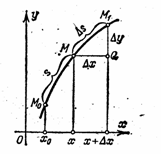 3). При изменении абсциссы x точки М длина s дуги будет меняться, т. е. s есть функция x. Найдём производную s по x.
3). При изменении абсциссы x точки М длина s дуги будет меняться, т. е. s есть функция x. Найдём производную s по x.
Дадим x приращение Dx. Тогда дуга s получит приращение Ds = дл. ÈMM1. Пусть ![]() - хорда, стягивающая эту дугу. Для того чтобы найти
- хорда, стягивающая эту дугу. Для того чтобы найти ![]() , поступим следующим образом:
, поступим следующим образом:
Из DMM1Q находим ![]() = (Dx)2 +(Dy)2. Умножим и разделим левую часть наDs2:
= (Dx)2 +(Dy)2. Умножим и разделим левую часть наDs2:

Разделим все члены равенства на Dx2:
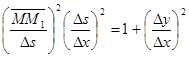
Найдём предел левой и правой частей при Dx®0. Учитывая, что ![]() и
и ![]() , получим
, получим 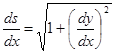
Для дифференциала дуги получим следующее выражение:
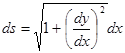 или
или ![]()
Мы получили выражение дифференциала дуги для того случая, когда кривая задана уравнением y=f(x). Но эта же формула сохраняется и в том случае, когда кривая задана параметрически:
![]()
![]()
и выражение принимает вид: ![]() .
.
Кривизна
Первая производная функции даёт нам простейшую характеристику линии y=f(x), а именно её направление. Вторая производная тесно связана с другой количественной характеристикой этой линии, с так называемой кривизной, устанавливающей меру изогнутости или искривлённости линии.
Пусть мы имеем кривую, которая не пересекает сама себя и имеет определённую касательную в каждой точке. Проведём касательные к кривой в каких-нибудь двух её точках А и В и обозначим через a угол, образованный этими касательными, или – точнее - угол поворота касательной при переходе от точки А к точке В (рис. 4). Этот угол называется углом смежности. Угол смежности в некоторой степени даёт представление о степени изогнутости дуги. У двух дуг, имеющих одинаковую длину, больше изогнута та, у которой угол смежности больше (рис. 5,4).
 рис. 4
рис. 4  рис. 5
рис. 5
Полной характеристикой изогнутости кривой будет отношение угла смежности к длине соответствующей дуги.
Определение 4. Средней кривизной Кср дуги ÈАВ называется отношение соответствующего угла смежности a к длине дуги:
![]()
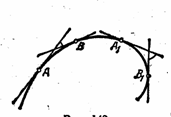
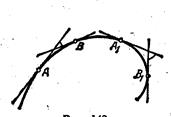 Для одной и той же кривой средняя кривизна её различных частей (дуг) может быть различной; так, например, для кривой (см. рис. 6) средняя кривизна дуги АВ не равна средней кривизне дуги А1В1 , хотя длины этих дуг равны между собой.
Для одной и той же кривой средняя кривизна её различных частей (дуг) может быть различной; так, например, для кривой (см. рис. 6) средняя кривизна дуги АВ не равна средней кривизне дуги А1В1 , хотя длины этих дуг равны между собой.
Отметим, что вблизи различных точек кривая искривлена по-разному. Для того чтобы охарактеризовать степень искривлённости данной линии в непосредственной близости к данной точке А, введём понятие кривизны в данной точке.
Определение5. Кривизной Ка линии в данной точке А называется предел средней кривизны дуги АВ, когда длина этой дуги стремится к нулю:
![]()
Вычисление кривизны
Выведем формулу для вычисления кривизны данной линии в любой её точке M(x, y). При этом будем предполагать, что кривая задана в декартовой системе координат уравнением вида y=f(x) и что функция имеет непрерывную вторую производную.
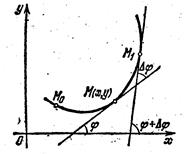 Проведём касательные к кривой в точках M и M1 с абсциссами x и x+Dx и обозначим через j и j+Dj углы наклона этих касательных (рис.7).
Проведём касательные к кривой в точках M и M1 с абсциссами x и x+Dx и обозначим через j и j+Dj углы наклона этих касательных (рис.7).
