Реферат: Кривизна плоской кривой Эволюта и эвольвента

Эвольвентное зацепление предложено математиком Л. Эилером.

Примеры

1. Найдём кривизну параболы y = x2 в любой её точке.

Имеем: и . Поэтому ; в частности кривизна параболы в её вершине равна 2.

2. Найдём кривизну прямой y = ax + b в её произвольной точке.

По формуле вычисления кривизны получаем результат К=0, означающий, что прямая представляет собой «линию нулевой кривизны».

3. Найдём уравнения эволюты параболы y = x2 .

Найдём значения X и Y: ,

Исключив параметр x, найдём уравнение эволюты в явном виде:

4. Определим кривизну циклоиды в её произвольной точке.

Подставив полученные выражения в формулу 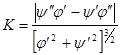, получим:

.

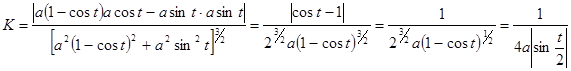5. Найдём уравнение эволюты эллипса, заданного параметрическими уравнениями

Вычислим производные от x и y по t:

Подставим данные значения в формулы и :

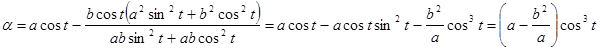
Аналогично получаем значение b: .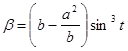

Исключая параметр t, получаем уравнение эволюты эллипса с текущими координатами a и b в виде .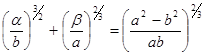

Список литературы

Н. С. Пискунов, Дифференциальное и интегральное исчисления, т. 1, «Наука», 1985.

А. Ф. Бермант, И. Г. Араманович, Краткий курс математического анализа, «Наука», 1966.

Е. Е. Иванова, Дифференциальное исчисление функций одного переменного, Издательство МГТУ им. Баумана, 1999.

В. А. Ильин, Э. Г. Позняк, Основы математического анализа, ч. 1, «Наука», 1982.

Б. П. Демидович, Задачи и упражнения по математическому анализу, «Интеграл – пресс», 1997.