Реферат: Кривизна плоской кривой Эволюта и эвольвента

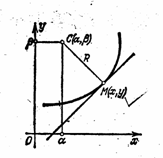
Так как точка C(a, b) лежит на нормали, то её координаты должны удовлетворять уравнению .

Далее, точка C(a, b) находится от точки М на расстоянии, равном радиусу кривизны R:

Решив совместно уравнения * определим a, b:

и так как , то

Чтобы решить вопрос о том, верхние или нижние знаки сле6дует брать в последних формулах, нужно рассмотреть случай y!!>0 и y!!<0. Если y!!>0 , то в этой точке кривая вогнута и, следовательно, b>y (рис. 9) и поэтому следует брать нижние знаки. Учитывая, что в этом случае ½y!!½= y!!, формулы координат центра запишем в следующем виде:

(1)

Аналогично можно показать, что формулы будут справедливы и в случае y!!<0.

Параметрическое задание кривой

Если кривая задана параметрически: x = j(t), y = y(t), то координаты центра кривизны можно получить из формул *, подставляя в них вместо y! и y!! их выражения через параметр:

.

Тогда

(2)

Эволюта и эвольвента

Если в точке M1(x, y) данной линии кривизна отлична от нуля, то этой точке соответствует вполне определённый центр кривизны C1(a, b) . Совокупность всех центров кривизны данной линии образует некоторую новую линию, называемую эволютой по отношению к первой.

По отношению к своей эволюте данная линия называется эвольвентой или инволютой (или развёрткой). Дадим определение.

Определение 8. Геометрическое место центров кривизны линии L называется её эволютой L1 , а сама линия L относительно своей эволюты называется эвольвентой.

Если данная кривая определяется уравнением y=f(x) , то уравнения (1) можно рассматривать как параметрические уравнения эволюты с параметром x. Исключая из этих уравнений параметр x, получим непосредственную зависимость между текущими координатами эволюты a и b. Если же кривая задана параметрически x = j(t), y = y(t), то уравнеия (2) дают параметрические уравнеия эволюты.

Свойства эволюты

Теорема 1. Нормаль к данной кривой является касательной к её эволюте.

Доказательство. Угловой коэффициент касательной к эволюте, определяемой параметрическими уравнениями (1) , равен . В силу уравнений (1)

, (3)

(4)

Получаем соотношение

.

Но y! есть угловой коэффициент касательной к кривой в соответствующей точке, поэтому из полученного соотношения следует, что касательная к кривой и касательная к её эволюте в соответствующей точке взаимно перпендикулярны, то есть нормаль к кривой является касательной к эволюте.

Теорема 2. Если на некотором участке M1M2 кривой радиус кривизны изменяется монотонно, то приращение длины дуги эволюты на данном участке кривой равно по абсолютной величине соответствующему приращению радиуса кривизны данной кривой.

Доказательство.