Реферат: Логика. Формальная или диалектическая?

Чудо!?

Диво! (Удивиться - оказаться у дива. "...Удивление побуждает людей философствовать..."[8.69]. Диво есть процесс творения, суть из ничего нечто).

""Н е т" (курсив Гегеля) "ничего ни... в природе, ни в духе, ни где бы то ни было, что не содержало бы вместе и непосредствен­ности и опосредствования""[9.92].

Далеко не случайно, что именно Архимед начал впервые созна­тельно применять дифференциальное исчисление, хотя еще его "ме­тод носит только частный характер"[18.505].

"Треугольник" Л.Выготского осуществляется задолго до рождения самого Л.Выготского. Осуществляется и при его жизни и после неё. Закон. Объективная реальность, которую ученые не в силах еще рас­смотреть (или принять!?).

"Все эти процессы и все эти методы мышления не укладываются в рамки метафизического мышления. Для диалектики же, для которой существенно то, что она берет вещи и их умственные отражения в их взаимной связи, в их сцеплении, в их движении, в их возникновении и исчезновении, - такие процессы, как вышеуказанные, напротив, лишь подтверждают её собственный метод исследования. Природа яв­ляется пробным камнем для диалектики, и надо сказать, что совре­менное естествознание доставило для такой пробы чрезвычайно бога­тый, с каждым днем увеличивающийся материал и этим материалом до­казано, что в природе все совершается в конечном счете диалекти­чески, а не метафизически. Но так как и до сих пор можно по паль­цам перечесть естествоиспытателей, научившихся мыслить диалекти­чески (т. е. сознательно применять диалектический метод при поис­ке решения. Авт.), то этот конфликт между достигнутыми и укорени­вшимся способом мышления вполне объясняет ту безграничную путани­цу, которая господствует теперь в теоретическом естествознании и одинаково приводит в отчаяние как учителей, так и учеников, как писателей, так и читателей"[19.19-22].

"Мысль рождается как ересь, а умирает как заблуждение" (Гегель).

Математике долгое время удавалось скрывать в cвоей утробе диа­лектику. Формальная логика категорически запрещает противоречие, диалектику, развитие, движение, творчество, революцию. Математики клятвенно утверждают, что "двигаться могут только материальные тела (материальная точка, материальная линия и пр.). Геометричес­кие же фигуры в научной геометрии суть "объекты чистого мышления, которые не могут быть передвигаемы""[13.49].

Математики допускают две существенные ошибки. Во-первых, геоме­трические фигуры не являются "объектами чистого мышления". Во­-вторых, математикики не ведают природы и сути мышления (мысли).

Уже который раз естествознание натыкается на факт, который взрывает основной закон формальной логики. Впервые с этим фактом ученые столкнулись при открытии Ньютона - Лейбница диффиренциаль­ного и интегрального исчисления. Математика, родная сестра форма­льной логики, первой ""совершила грехопадение"(Энгельс Фр.)"[20. 6].

Здесь мы полностью приводим "appendix" К.Маркса. "В этом при­ложении Маркс объясняет Энгельсу на примере задачи о касательной к параболе сущность дифференциального исчисления"[20.251]. Здесь, даже не имеющему серьезного математического образования, уже мож­но указать на взрыв основного закона формальной логики.

""Приложение"

Ты как-то просил меня во время моего последнего пребывания в Манчестере объяснить дифференциальное исчисление. На следующем примере ты сможешь полностью уяснить себе этот вопрос. Все диффе­ренциальное исчисление возникло первоначально из задачи о прове­дении касательных к произвольной кривой через любую ее точку. На этом же примере я и хочу пояснить тебе существо дела.

Пусть линия mAo - произвольная кривая, природы которой (явля­ется ли она параболой, эллипсом и т. д.) мы не знаем и где в точ­ке m требуется провести касательную.

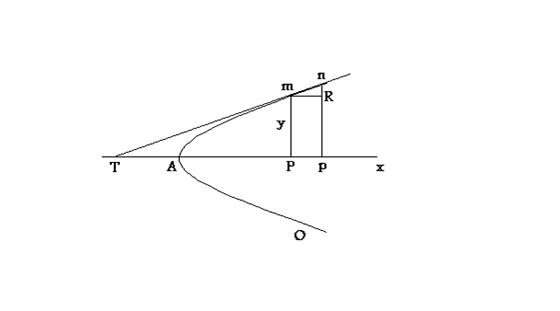
Рис. 4

Ах - ось. Мы опускаем перпендикуляр mP (ординату) на абсцис­су Ах . Представь себе теперь, что точка n - бесконечно ближай­шая точка кривой возле m . Если я опущу на ось перпендикуляр np , то р должна быть бесконечно ближайшей точкой к Р , а np - бес­конечно ближайшей параллельной линией к mP . Опусти теперь беско­нечно малый перпендикуляр mR на np . Если ты теперь примешь аб­сциссу АР за х, а ординату mP за у , то np = mP (или Rp ), увеличенной на бесконечно малое приращение [nR] , или [nR] = dy (дифференциал от у ), а mR = (Pp) = dx . Так как часть mn каса­тельной бесконечно мала, то она совпадает с соответствующей час­тью самой кривой. Я могу, следовательно, рассматривать mnR как D (треугольник), D-ки же mnR и mTP - подобные треугольники. Поэтому dy (= nR):dx(= mR) = y (= mP):PT (которое есть подкаса­тельная для касательной Tn). Следовательно, подкасательная

dx

РТ = y .

dy

Это и есть общее дифференциальное уравнение для всех точек касания всех кривых. Если мне теперь нужно дальше оперировать с этим уравнением и с его помощью определить величину подкасатель­ной РТ (имея последнюю, мне остается только соединить точки Т и m прямой линией, чтобы получить касательную), то я должен знать, каков специфический характер кривой. В соответствии с ее характером (как парабола, эллипс, циссоида и т. д.) она имеет определенное общее уравнение для ее ординаты и абсциссы каждой точки, которое известно из алгебраической геометрии. Если, напри­мер, кривая mAo есть парабола, то я знаю, что у² (y - ордината каждой произвольной точки) = ах, где а - параметр параболы, а х - абсцисса, соответствующая ординате у.

Если я подставлю это значение для у в уравнение

dx

РТ = y ,

dy

то я должен, следовательно, искать сначала dy, т. е. найти диффере­нциал от у (выражение, которое добавляется к у при его бесконе­чно малом возрастании). Если y² = ax, то я знаю из дифференци­ального исчисления, что d(y² ) = d(ax) (я должен, разумеется, дифференцировать обе части уравнения) дает 2y dy = a dx (d везде обозначает дифференциал). Следовательно,

2ydy

dx = .

a

Если я подставлю это значение для dx в формулу

ydx