Реферат: Магнитные свойства атомов
ΔΕlS ~ 1/n3 .
Существование механического (спина) и магнитного моментов у электрона и объяснение их свойств вытекает из релятивистской квантовой механики, из основного ее уравнения – уравнения Дирака. В частности, из релятивистской квантовой механики следуют соотношения (15), (16), (17), справедливость которых, как и существование спина, подтверждается экспериментами.
В экспериментах обычно подтверждается не сам магнитный момент микросистемы, а его проекция. Согласно (17), сколько ms = ![]() 1/2, проекция собственного магнитного момента электрона по абсолютной величине равна одному магнетону Бора
1/2, проекция собственного магнитного момента электрона по абсолютной величине равна одному магнетону Бора
![]() s H = 2 m0 ms =
s H = 2 m0 ms = ![]()
![]() 0.
0.
Часто под собственным магнитным моментом электрона подразумевают не его значение (15), а значение его проекции (17) и говорят, что электрон обладает магнитным моментом, равным по абсолютной величине одному магнетону Бора.
§3. Полный магнитный момент одноэлектронного атома
До сих пор мы рассматривали поведение орбитального ![]() l и спинового
l и спинового ![]() S магнитных моментов электрона во внешнем магнитном поле в предположении отсутствия взаимодействия между ними. Однако, в отсутствии внешнего магнитного поля между этими моментами существует взаимодействие, в результате которого имеют место взаимодействия между орбитальным
S магнитных моментов электрона во внешнем магнитном поле в предположении отсутствия взаимодействия между ними. Однако, в отсутствии внешнего магнитного поля между этими моментами существует взаимодействие, в результате которого имеют место взаимодействия между орбитальным ![]() l и спиновым
l и спиновым ![]() s моментами количества движения электрона (ls - взаимодействие). При этом векторы
s моментами количества движения электрона (ls - взаимодействие). При этом векторы ![]() l и
l и ![]() s прецессируют относительно вектора полного момента количества движения
s прецессируют относительно вектора полного момента количества движения ![]() J численно равного
J численно равного
|![]() J | = (h / 2π)
J | = (h / 2π) ![]() , (19)
, (19)
где внутренне квантовое число j принимает одно из значений j = l+s; l+s-1;… …(l-s).
|![]() l | = (h / 2π)
l | = (h / 2π) ![]() =
=![]() l* ,
l* ,
|![]() s | = (h / 2π)
s | = (h / 2π) ![]() =
=![]() S* ,
S* ,
|![]() J | = (h / 2π)
J | = (h / 2π) ![]() =
=![]() j* .
j* .
Схема суммирование векторов ![]() l и
l и ![]() s .
s .

Причем проекция полного момента количества движения![]() J , на какое-либо направление равна
J , на какое-либо направление равна ![]() JZ = (h / 2π) mj, где mj = j; j-1; ……, -j, т.е. mJ принимает 2j+1 значений. Т.к. у электрона помимо моментов
JZ = (h / 2π) mj, где mj = j; j-1; ……, -j, т.е. mJ принимает 2j+1 значений. Т.к. у электрона помимо моментов ![]() l и
l и ![]() s есть еше магнитные моменты: орбитальный
s есть еше магнитные моменты: орбитальный ![]() l и собственный
l и собственный ![]() S , направленный противоположно соответствующим моментам количества движения, то рис.2 необходимо дополнить векторами
S , направленный противоположно соответствующим моментам количества движения, то рис.2 необходимо дополнить векторами ![]() l и
l и ![]() S (см. рис. 3). При этом необходимо учесть, что отношение μS / PS вдвое больше отношения μ1 / P1 . Поэтому, если на рис. 3 вектор
S (см. рис. 3). При этом необходимо учесть, что отношение μS / PS вдвое больше отношения μ1 / P1 . Поэтому, если на рис. 3 вектор ![]() l изобразить равным по длине вектору
l изобразить равным по длине вектору ![]() l , то в том же масштабе длина вектора μS должна быть в два раза больше длины вектора
l , то в том же масштабе длина вектора μS должна быть в два раза больше длины вектора ![]() s , рис.3 выполнен с учетом этого обстоятельства. Из рис. видно, что вследствие того что, μS / PS
s , рис.3 выполнен с учетом этого обстоятельства. Из рис. видно, что вследствие того что, μS / PS ![]() μ1 / P1 направление вектора результирующего магнитного момента
μ1 / P1 направление вектора результирующего магнитного момента ![]() (
(![]() = μS +μ1 – полного магнитного момента атома) не совпадает с направлением вектора полного магнитного момента количества движения
= μS +μ1 – полного магнитного момента атома) не совпадает с направлением вектора полного магнитного момента количества движения ![]() J . Векторы
J . Векторы ![]() l и
l и ![]() s прецессируют вокруг направления того же вектора.
s прецессируют вокруг направления того же вектора.
Схема суммирование векторов ![]() l и
l и ![]() S.
S.
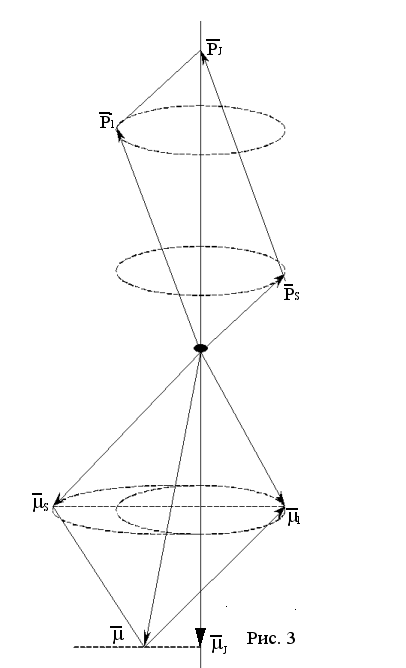
Усредненное значение перпендикулярных составляющих обоих магнитных моментов за прецессии будет равно нулю, т.к. эти составляющие непрерывно меняют свое направление в пространстве.
Т.о., эффективный полный магнитный момент одноэлектродного атома будет равняться сумме параллельных составляющих векторов ![]() l и
l и ![]() S , т.е. будет равен вектору
S , т.е. будет равен вектору ![]() J . Следовательно, полный магнитный момент атома (в отсутствии внешнего магнитного поля) равен (см. рис. 3).
J . Следовательно, полный магнитный момент атома (в отсутствии внешнего магнитного поля) равен (см. рис. 3).
![]() J = μ1 Cos (
J = μ1 Cos (![]() l
l ![]() J ) + μS Cos (
J ) + μS Cos (![]() S
S ![]() J ) (21)
J ) (21)
| ![]() l | = (h / 2π) l* ; |
l | = (h / 2π) l* ; |![]() l | =
l | = ![]() 0 l* ;
0 l* ;
| ![]() J | = (h / 2π) j* ; |
J | = (h / 2π) j* ; |![]() S | =
S | = ![]() 0 S* ;
0 S* ;
| ![]() S | = (h / 2π) S* ;
S | = (h / 2π) S* ;
На рисунке 3, на основании известной тригонометрической формулы, следует, что
Cos (![]() l
l ![]() J ) = (l (l +1) + j (j +1) – s (s + 1)) / 2
J ) = (l (l +1) + j (j +1) – s (s + 1)) / 2 ![]()
![]()
Cos (![]() S
S ![]() J ) = (s (s +1) + j (j +1) – l (l + 1)) / 2
J ) = (s (s +1) + j (j +1) – l (l + 1)) / 2 ![]()
![]() (22)
(22)
Подставляя (8), (15), (22) в (21), получим
μJ = μ0 (3 j (j + 1) + s (s +1) – l (l + 1)) / (2![]() ) (23)
) (23)
Умножая числитель и знаменатель на ![]() , приводим выражение (23) к виду
, приводим выражение (23) к виду
μJ = μ0 ![]() {1 + (j (j + 1) + s (s + 1) - l (l + 1)) / 2j (j + 1)} (24)
{1 + (j (j + 1) + s (s + 1) - l (l + 1)) / 2j (j + 1)} (24)
Величина g = 1 + (j (j + 1) + s (s + 1) - l (l + 1)) / 2j (j + 1) (25)
Называется множителем (фактором) Ланде, во многих явлениях играет важную роль.