Реферат: Магнитные свойства атомов

Следовательно, возможны только две ориентации магнитного момента атома серебра в S - состоянии относительно поля H.

Со стороны поля H, согласно (31) будет действовать сила либо ₁ = μ₀ (dx), либо ₂ = - μ₀ (dx). Поэтому одни атомы смещаются в сторону возрастания поля, другие – в сторону уменьшения напряженности , вследствие чего пучок расщепляется на две компоненты, что подтверждилось на опыте.

Поэтому в S - состоянии l=0, то μ_l = 0 (μ_l = (e /2mC)P_l ), следовательно, магнитный момент атома серебра в основном состоянии обусловлен собственным магнитным моментом электрона, и было определено в 1952 г.

μ_SH = 1.00116 μ₀ ,

а не μ_SH = 2μ₀ m_s = μ₀ , что следует из релятивистского уравнения Шредингера, уравнения Дирака. Это получило специальное название – аномального магнитного электрона. Аномальный магнитный момент электрона обусловлен его взаимодействием с собственным электромагнитным полем.

Эффект Зеемана

Является убедительным экспериментальным доказательством существования магнитного атомного момента и его пространственного квантования.

Если свет от источника рассматривать в направлении перпендикулярном магнитному полю (вдоль оси У), то каждая линии расщеплена и состоит из трех компонентов:

ν₀ ; ν₀ + Δν; ν₀ – Δν; где ν₀ – частота линии в отсутствие магнитного поля;

Δν0 = eH / 4πmC;

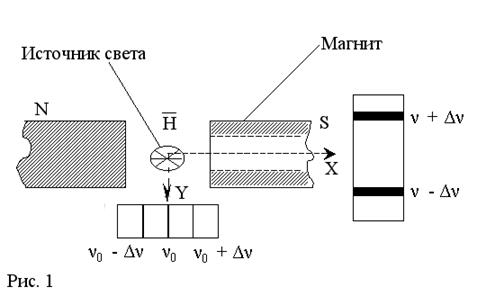
H – напряженность внешнего магнитного поля.

Если свет рассматривать вдоль направления магнитного поля (вдоль оси Х), то каждая расщепится только на две компоненты:

ν₀ + Δν; ν₀ – Δν.

В отсутствие магнитного поля атом находится в состоянии с энергией E_Y . Поместим его во внешнее поле . Появляется связь _l - _s – магнитное взаимодействие и взаимодействие _l - и _s - . Если слабое, то последнее взаимодействие сильное. Энергия атома в магнитном поле изменится за счет потенциальной энергии ΔΕΗ взаимодействия магнитного момента атома с магнитным полем и сделается равной EIH = EI + ΔΕΗ.

ΔΕΗ – потенциальная энергия взаимодействия магнитного момента атома _l с внешним магнитным полем равна

ΔΕΗ = μ₀ g H M_I

где M_I – полное магнитное квантовое число при данном J имеет 2I + 1 значений, то есть M_I = I, I – 1, I – 2, …- I. Таким образом, в слабом магнитном поле каждый энергетический уровень E_I (каждый терм) атома расщепится на 2J + 1 подуровней с энергиями

E_JH = E_J + μ₀ g H M_I.

Обычно, расщепление энергетических уровней атома в магнитном поле называют зеемановским расщеплением .

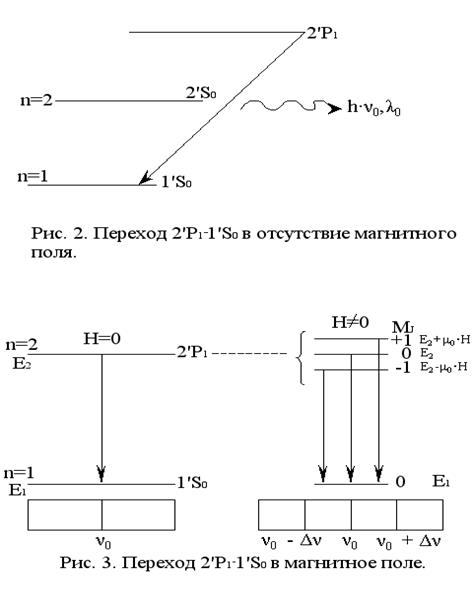
Энергетический уровень 2’P_l в магнитном поле расщепится на 3 подуровня. В 2’P_l состоянии L=1, S=0, I=0, то магнитное квантовое число M_I принимает три значения –

M_τ = +1; 0; -1.

Множитель Ланде для 2’P_l :

g₂ = 1 + (I (I + 1) + S (S + 1) - L (L + 1)) / 2I (I + 1))=1

В состоянии 2’P_l атом гелия в магнитном поле обладает энергетическими подуровнями:

E’_{2 H} = E₂ + μ₀ H (M=1),

E’’_{2 H} = E₂ (M=0),

E’’’_{2 H} = E₂ - μ₀ H (M= - 1),

То есть уровень 2’P_l с энергией Ε₂ в магнитном поле расщепится на три подуровня с энергиями E’_{2 H} , E’’_{2 H} , E’’’_{2 H} . Согласно правилам отбора ΔL = 1; ΔS = 0; ΔI = 0, 1; ΔM_I = 0, 1 при переходе 2’P_l - 1’S₀ , в магнитном поле вместо одной линии λ₀ будет излучаться три линии: λ₁ , λ₂ = λ₀ , λ_3.

Причем линии, для которых ΔM_I = 0 (π - компоненты) согласно квантовой механике будут поляризованы линейно, то есть так, что электрический вектор расположен параллельно полю .

Линии, для которых ΔM_I = 1 (σ - компоненты), будут поляризованы так, что электрический вектор их волны расположен перпендикулярно полю и будут обладать круговой поляризацией (по правому и левому кругу).