Реферат: Магнитные свойства атомов

μ_J = μ₀ g = μ₀ gj^* (26)

Если поместить атом в “слабое” магнитное поле, “слабое” настолько, чтобы взаимодействие моментов _l и _S между собой было значительно больше их взаимодействия с внешним магнитным полем. То есть в этом случае атом будет вести себя в поле как магнитный диполь с моментом, равным _l . Причем этот момент будет ориентирован относительно поля определенным образом. А именно так, чтобы проекция вектора _J на направление поля принимала значения

P_JH = P_J Cos (_J ) = h / 2πm_J , (27)

m_J = j, j-1, ……,- j. Cos (_J ) = m_J / j^* .

И соответственно проекция магнитного момента атома μ_JH на направление внешнего магнитного поля будет равна.

μ_JH = μ_J Cos (_J ) = μ_J (m_J / j^* ) = μ₀ gm_J (28)

Дополнительная потенциальная энергия взаимодействия магнитного момента атома с внешним магнитным полем будет равна

ΔΕ = ( _l ) = μ_J HCos (_J ) = μ₀ gHm_J (29)

Векторы _l , _s , _J ориентируются определенным образом в пространстве относительно направления магнитного поля, что называется “пространственным квантованием“.

§4. Опыты Штерна и Герлаха

На пролетающие через неординарное магнитное поле атомы будет действовать не только момент сил, стремящийся повернуть их магнитные моменты в направлении поля, но будет действовать отклоняющая сила, обусловленная неодинаковой напряженностью магнитного поля у полюсов атомного магнитного диполя.

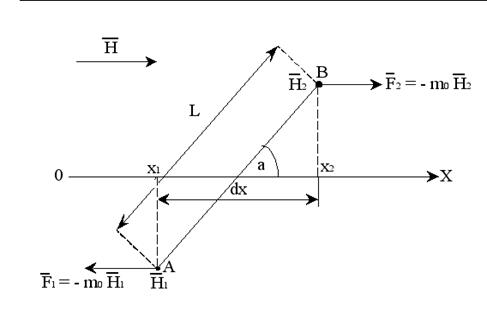
Пусть m₀ – величина “магнитного заряда“, сосредоточенного в каждом из полюсов атомного магнитного диполя. H₁ и H₂ – напряженность магнитного поля в точках A и B. Сила, действующая на диполь со стороны поля в направлении OX, равна F_X = F₂ – F₁ = m₀ (H₂ – H₁ ) = m₀ (dH / dx) dx.

dx = L cosα

F_X = m₀ L dH / dx Cosα,

μ = m₀ L – магнитный момент диполя.

F_X = μ dH / dx Cosα (30)

В зависимости от ориентации магнитного момента (угол α), диполь будет смещается вдоль оси ОХ (т.е. вдоль поля) либо в сторону увеличения напряженности магнитного поля.

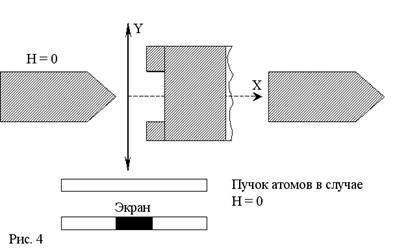
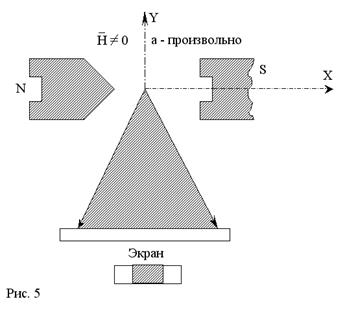
Рис.5

Если атомы обладают магнитными моментами, которые могут произвольно ориентироваться относительно поля, то узкий первоначальный пучок атомов, летящий вдоль оси OY, пересекая неоднородное магнитное поле, направленное вдоль оси OX, растянется в широкую (в направлении поля) полосу, в соответствии с произвольными значениями cosα в пределах

-1cosα1.

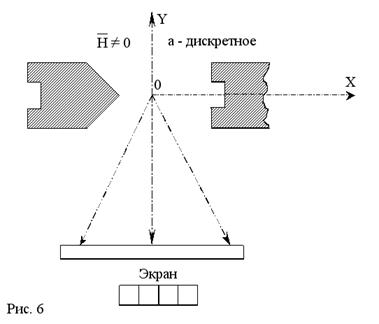
Рис. 6

Если магнитные моменты атомов могут ориентироваться относительно направления поля только вполне определенным образом, т.е. cosα может принимать только вполне определенные дискретные значения, то в соответствии с этим первоначальный пучок должен расщепиться на ряд компонент. Как следует из вывода соотношения (30).

Опыты могут доказать не только существование магнитного момента у атома, но и проверить достоверность выводов теории пространственного квантования.

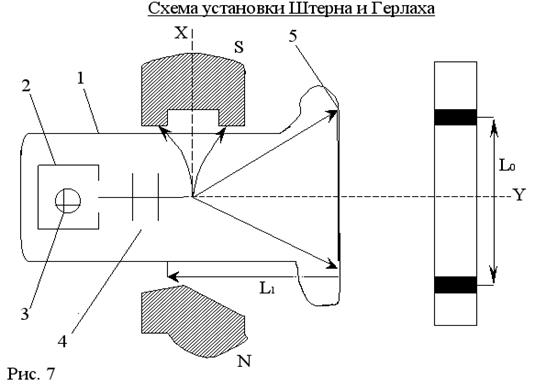
В откачанном до глубокого вакуума сосуде 1 помещена маленькая печь 2, в которой находится кусочек серебра 3. При нагревании печи серебро испаряется, атомы Ag вылетают из печи во всех возможных направлениях с тепловыми скоростями (~ несколько сотен м/с). Несколько щелей 4 выделяют узкий пучок атомов серебра, летящий вдоль оси Y. Атомный пучок пролетает через область неоднородного магнитного поля, направленного вдоль оси X. На пластине 5, пучок конденсируется на ней. Атомный пучок расщепляется, что подтверждает справедливость теории пространственного квантования, доказано наличие у атомов магнитного момента.

Полный магнитный момент атома μ_J = μ₀ gj^* ,

его проекция μ_JH = μ₀ gm_J ,

где квантовое число m_J = j, j - 1, …, - j.

Отклоняющая сила

F_X = μ₀ g (dH / dx) m_J

Все атомы серебра находятся в основном состоянии ² S₄ , орбитальным l = 0, спином S = ½, внутренним j = ½, множитель Ланде

g = 1 + (j (j + 1) + s (s + 1) - l (l + 1)) / 2j (j + 1)) = 2