Реферат: Математическая статистика
Вывод : 
при данном уровне значимости гипотеза не отвергается.
Задача 4.118
Из n1 = 200 задач первого типа, предложенных для решения, студенты решили m1 = 152, а из n2 = 250 задач второго типа студенты решили m2 = 170 задач. Проверить на уровне значимости a = 0.05 гипотезу о том, что вероятность решения задачи не зависит от того, к какому типу она относится, т.е. H0 : P1 = P2 . В ответе записать разность между абсолютными величинами табличного и фактического значений выборочной характеристики.
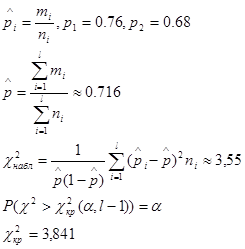
Вывод: 
нулевая гипотеза при данном уровне значимости принимается (
).
Задача 1.39:
Вычислить центральный момент третьего порядка (m3 * ) по данным таблицы:
| Урожайность (ц/га), Х | 34,5-35,5 | 34,5-36,5 | 36,5-37,5 | 37,5-38,5 | 38,5-39,5 |
| Число колхозов, mi | 4 | 11 | 20 | 11 | 4 |
Решение:
| Урожайность (ц/га), Х | Число колхозов, mi | Xi | mi xi | (xi -x ср )3 | (xi -x ср )3 mi |
| 34,5-35,5 | 4 | 35 | 140 | -8 | -32 |
| 34,5-36,5 | 11 | 36 | 396 | -1 | -11 |
| 36,5-37,5 | 20 | 37 | 740 | 0 | 0 |
| 37,5-38,5 | 11 | 38 | 418 | 1 | 11 |
| 38,5-39,5 | 4 | 39 | 156 | 8 | 32 |
| Итого: | 50 | - | 1850 | - | 0 |
 |
 |
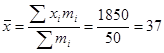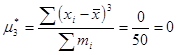Ответ: m3 * =0
Задача 2.34:
В результате анализа технологического процесса получен вариационный ряд:
| Число дефектных изделий | 0 | 1 | 2 | 3 | 4 |
| Число партий | 79 | 55 | 22 | 11 | 3 |
Предполагая, что число дефектных изделий в партии распределено по закону Пуассона, определить вероятность появления 3 дефектных изделий.
Решение:
| m | 0 | 1 | 2 | 3 | 4 |
| p | 0.4647 | 0.3235 | 0.1294 | 0.0647 | 0.0176 |
Ответ: P=7.79*10-7
Зпадача 3.28:
В предложении о нормальной генеральной совокупности с s=5 сек., определить минимальный объем испытаний, которые нужно провести, чтобы с надежностью g=0.96 точность оценки генеральной средней m времени обработки зубчатого колеса будет равна d=2 сек.
 |
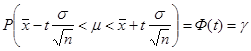Решение:
 |
n=(5.1375)3 =26.39?27
Ответ: n=27
Задача 3.48:
На основании измерения n=7 деталей вычислена выборочная средняя и S=8 мк. В предположении, что ошибка изготовления распределена нормально, определить с надежностью g=0.98 точность оценки генеральной средней.
Решение:
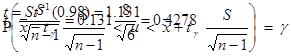
St(t,n=n-1)=g=St(t,6)=0.98
Ответ: d=0.4278
Задача 3.82:
На основании n=4 измерений температуры одним прибором определена S=9°С. Предположив, что погрешность измерения есть нормальная случайная величина определить с надежностью g=0.9 нижнюю границу доверительного интервала для дисперсии.
Решение:
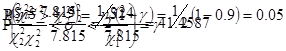
Ответ: 41.4587
Задача 3.103:
Из 400 клубней картофеля, поступившего на контроль вес 100 клубней превысили 50 г. Определить с надежностью g=0.98 верхнюю границу доверительного интервала для вероятности того, что вес клубня превысит 50 г.
Решение: