Реферат: Математическая статистика
![]()
Ответ: 0.3
Задача 3.142:
По результатам 100 опытов установлено, что в среднем для сборки вентиля требуется Xср =30 сек., а S=7 сек. В предположении о нормальном распределении определить с надежностью g=0.98 верхнюю границу для оценки s генеральной совокупности.
Решение:
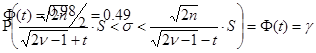
t=2.33
![]()
Ответ: 8.457
Задача 4.18:
Гипотезу о нормальном законе распределения проверить с помощью критерия Пирсона на уровне значимости a=0.05 по следующим данным:
| mi | 6 | 13 | 22 | 28 | 15 | 3 |
| mi T | 8 | 17 | 29 | 20 | 10 | 3 |
Решение:
| mi | mi T | (mi -mi T )2 | (mi -mi T )2 / mi T |
| 6 | 8 | 4 | 0.5 |
| 13 | 17 | 16 | 0.941 |
| 22 | 29 | 49 | 1.6897 |
| 28 | 20 | 64 | 3.2 |
| 10 | 25 | 1.9231 | |
| 3 | 3 | ||
| Итого: | - | - | 8.2537 |
![]()
Ответ: -2.2627
1.36.
Вычислить дисперсию.
| Производительность труда | Число рабочих | Средняя производительность труда |
| 81,5-82,5 | 9 | 82 |
| 82,5-83,5 | 15 | 83 |
| 83,5-84,5 | 16 | 84 |
| 84,5-85,5 | 11 | 85 |
| 85,5-86,5 | 4 | 86 |
| Итого | 55 |
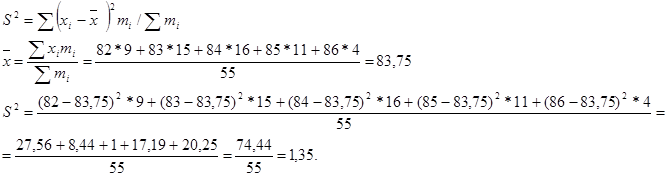 |
2.19.
Используя результаты анализа и предполагая, что число дефектных изделий в партии распределено по закону Пуассона, определить теоретическое число партий с тремя дефектными изделиями.
| m | 0 | 1 | 2 | 3 | 4 | 5 | Итого |
| fi | 164 | 76 | 40 | 27 | 10 | 3 | 320 |
| Pm | 0,34 | 0,116 | 0,026 | 0,004 | 0,001 | ||
| Pm*fi | 288,75 | 25,84 | 4,64 | 0,702 | 0,04 | 0,003 | 320 |
| fi теор. | 288 | 26 | 5 | 1 | 0 | 0 | 320 |
m – число дефектных изделий в партии,
fi – число партий,
fi теор. = теоретическое число партий
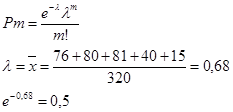
Теоретическое значение числа партий получается округлением Pm*fi .
Соответственно, теоретическое количество партий с тремя дефектными изделиями равно 1.
3.20.
По выборке объемом 25 вычислена выборочная средняя диаметров поршневых колец. В предложении о нормальном распределении найти с надежностью γ=0,975 точность δ , с которой выборочная средняя оценивает математическое ожидание, зная, что среднее квадратическое отклонение поршневых колец равно 4 мм ..
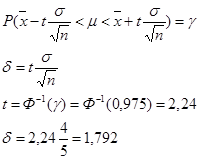
3.40.
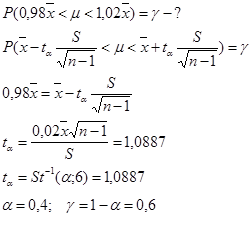 |
?? ??????????? ???? ????????? ??????? ?????? ??????????? ?????? ????? 40 мм ., ? S=1,8 мм.. ? ????????????? ? ?????????? ????????????? ?????????? ??????????? ????, ??? ??????????? ??????? ????? ?????? ????????? (0,98х;1,02х).
3.74.
По данным контрольных 8 испытаний определены х=1600 ч. и S=17ч..Считая, что срок службы ламп распределен нормально, определить вероятность того, что абсолютная величина ошибки определения среднего квадратического отклонения меньше 10% от S.
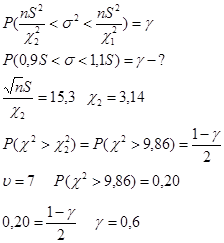
3.123.
По результатам 70 измерений диаметра валиков было получено х=150 мм., S=6,1 мм.. Найти вероятность того, что генеральная средняя будет находиться внутри интервала (149;151).
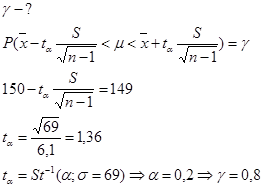
3.126