которое является регрессионной моделью (моделью регрессионного анализа). В этом выражении означает модельное, т.е. рассчитываемое по уравнению модели, значение выхода. Коэффициенты регрессии определяются экспериментально и служат для статистической оценки теоретических коэффициентов, т.е.

(4)

В регрессионной модели члены второй степени , характеризуют кривизну поверхности отклика. Чем больше кривизна этой поверхности, тем больше в модели регрессии членов высшей степени. На практике чаще всего стремятся ограничиться линейной моделью [1].

Эксперимент можно проводить по-разному. В случае, когда исследователь наблюдает за каким-то неуправляемым процессом, не вмешиваясь в него, или выбирает экспериментальные точки интуитивно, на основании каких-то привходящих обстоятельств, эксперимент считают пассивным. В настоящее время пассивный эксперимент считается неэффективным.

Гораздо более продуктивно проводится эксперимент, когда исследователь применяет статистические методы на всех этапах исследования, и, прежде всего, перед постановкой опытов, разрабатывая схему эксперимента, а также в процессе экспериментирования, при обработке результатов и после эксперимента, принимая решение о дальнейших действиях. Такой эксперимент считают активным, и он предполагает планирование эксперимента.

Под планированием эксперимента понимают процедуру выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью.

Под математической моделью планирования понимается наука о способах составления экономических экспериментальных данных планов, которые позволяют извлекать наибольшее количество информации об объекте исследования, о способах проведения эксперимента, о способах обработки данных и их использование для оптимизации производственных процессов, а также инженерных расчетов [3].

2. Краткая характеристика методики составления планов эксперимента для моделей первого и второго порядков

Использование теории планирования эксперимента является одним из путей существенного повышения эффективности многофакторных экспериментальных исследований. В планировании экспериментов применяются в основном планы первого и второго порядков. Планы более высоких порядков используются в инженерной практике редко. В связи с этим далее приводится краткое изложение методики составления планов эксперимента для моделей первого и второго порядков. Под планом первого порядка понимают такие планы, которые позволяют провести эксперимент для отыскания уравнения регрессии, содержащего только первые степени факторов и их произведения:

(5)

Планы второго порядка позволяют провести эксперимент для отыскания уравнения регрессии, содержащего и вторые степени факторов:

(6)

Нахождение уравнения регрессии методом планирования экспериментов состоит из следующих этапов:

· выбор основных факторов и их уравнений;

· планирование и проведение собственного эксперимента;

· определение коэффициентов уравнения регрессии;

· статистический анализ результатов эксперимента [1].

2.1 Общие положения о планировании второго порядка

Описание поверхности отклика полиномами первого порядка часто оказывается недостаточным. Во многих случаях удовлетворительная аппроксимация может быть достигнута, если воспользоваться полиномом второго порядка (6).

В этом случае требуется, чтобы каждый фактор варьировался не менее чем на трех уровнях. В этом случае полный факторный эксперимент содержит слишком большое количество опытов, равное . Так, при их 27, а число коэффициентов , при число опытов 243, а коэффициентов 21. В связи с этим осуществление полного факторного эксперимента (ПФЭ) для планов второго порядка не только сложно, но и нецелесообразно.

Сократить число опытов можно, воспользовавшись так называемым композиционным или последовательным планом, разработанным Боксом и Уилсоном. Так, при двух факторах модель функции отклика второго порядка представляет собой поверхность в виде цилиндра, конуса, эллипса и т.д., описываемую в общем виде уравнением:

. (7)

Для определений такой поверхности необходимо располагать координатами не менее трех ее точек, т.е. факторы и должны варьироваться не менее чем на трех уровнях. Поэтому план эксперимента в плоскости факторов и на рисунке 3, а не может состоять лишь из опытов 1, 2, 3, 4, располагающихся в вершинах квадрата, как это делается для модели первого порядка. К ним должны быть добавлены опыты (звездные точки) 5, 6, 7, 8, расположенные на осях и с координатами и обязательно опыт 9 в центре квадрата, чтобы по любому направлению (5-9-6), (1-9-4) и т.д. располагалось три точки, определяющие кривизну поверхности в этом направлении.

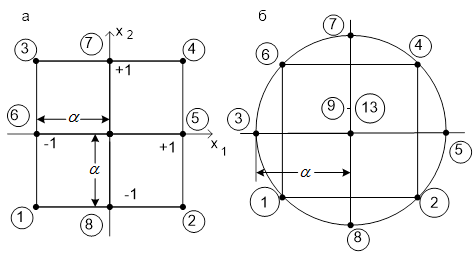
Рисунок 3 – Планы второго порядка при : а – ортогональный;

б – рототабельный

Таким образом, в общем случае ядро композиционного плана составляет при ПФЭ , а при - дробную реплику от него. Если линейное уравнение регрессии оказалось неадекватным, необходимо:

1) добавить (2 – k) звездных точек, расположенных на координатных осях факторного пространства где - звездное плечо, или расстояние до звездной точки;

2) провести опытов при значениях факторов в центре плана.

При kфакторах общее число опытов в матрице композиционного плана составит:

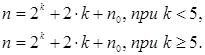(8)