Реферат: Математические методы планирования экспериментов
0
0
0
![]()
![]()
![]()
![]()
![]()
9
Аналогичным образом строятся планы и для большего числа факторов [1].
2.2 Ортогональные центральные композиционные планы второго порядка
В общем виде план, представленный в таблице 1, неортогонален так как
![]() (9)
(9)
Приведем его к ортогональному виду, для чего введем новые переменные (преобразования для квадратичных эффектов):
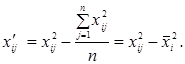 (10)
(10)
при этом
![]() (11)
(11)
Тогда уравнение регрессии будет записано как
![]() (12)
(12)
Композиционные планы легко привести к ортогональным, выбирая звездное плечо ![]() . В таблице 2 приведено значение а для различного числа факторов k и числа опытов в центре плана
. В таблице 2 приведено значение а для различного числа факторов k и числа опытов в центре плана ![]() .
.
Таблица 2 – Значения звездных плеч в ортогональных планах второго порядка
| Число опытов в центре плана | Звездное плечо | |||
|
(в ядре полуреплики) | ||||
| 1 | 1,000 | 1,215 | 1,414 | 1,546 |
| 2 | 1,077 | 1,285 | 1,471 | 1,606 |
| 3 | 1,148 | 1,353 | 1,546 | 1,664 |
| 4 | 1,214 | 1,414 | 1,606 | 1,718 |
| 5 | 1,267 | 1,471 | 1,664 | 1,772 |
| 6 | 1,320 | 1,525 | 1,718 | 1,819 |
| 7 | 1,369 | 1,575 | 1,772 | 1,868 |
| 8 | 1,414 | 1,623 | 1,819 | 1,913 |
| 9 | 1,454 | 1,668 | 1,868 | 1,957 |
| 10 | 1,498 | 1,711 | 1,913 | 2,000 |
В частности, ортогональный план второго порядка для ![]() и
и ![]()
![]() представлен в таблице 3, а его геометрическая интерпретация - на рисунке 3, а.
представлен в таблице 3, а его геометрическая интерпретация - на рисунке 3, а.
Представленный на рисунке 3, а и в таблице 3 прямоугольный (квадратный) план эксперимента для модели второго порядка работоспособен, хотя и несколько избыточен (9 опытов для определения 6 коэффициентов). Благодаря трем избыточным опытам, он позволяет усреднить случайные погрешности и оценить их характер.
Таблица 3 – Ортогональный центральный композиционный план второго порядка
| Номер опыта | Факторы | Результат | ||||||
|
Ядро плана |
1 2 К-во Просмотров: 685
Бесплатно скачать Реферат: Математические методы планирования экспериментов
| |||||||