Реферат: Математические методы планирования экспериментов
![]()
В этой таблице
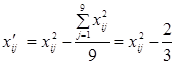 . (13)
. (13)
В силу ортогональности матрицы планирования ее коэффициенты равны:
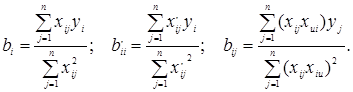 (14)
(14)
Уравнения регрессии ![]() определяются независимо один от другого по формулам.
определяются независимо один от другого по формулам.
Здесь i - номер столбца в матрице планирования; j - номер строки; суммы в знаменателях различны для линейных, квадратичных эффектов и взаимодействий.
Дисперсии коэффициентов уравнения регрессии следующие:
 . (15)
. (15)
Следует особо отметить, что коэффициенты уравнения регрессии, получаемые с помощью ортогональных планов второго порядка, определяются с разной точностью (см. уравнение (14)), в то время как ортогональные планы первого порядка обеспечивают одинаковую точность коэффициентов, т.е. план, представленный в таблице 3, являющийся ортогональным и обеспечивающий независимость определения коэффициентов b, не является рототабельным.
В результате расчетов по матрице с преобразованными столбцами для квадратичных эффектов получаем уравнение регрессии в виде:
![]() (16)
(16)
Для преобразования к обычной форме записи следует перейти от коэффициента ![]() к коэффициенту
к коэффициенту ![]() , используя выражение:
, используя выражение:
![]() . (17)
. (17)
При этом дисперсия этого коэффициента рассчитывается по следующему соотношению:
![]() (18)
(18)
В дальнейшем, зная дисперсию воспроизводимости, проверяют значимость коэффициентов и адекватность уравнения:
![]() (19)
(19)
Значимость коэффициентов проверяется по критерию согласия Стьюдента ![]() . Коэффициент значим, если
. Коэффициент значим, если ![]() , где m– число степеней свободы дисперсии воспроизводимости.
, где m– число степеней свободы дисперсии воспроизводимости.
Адекватность уравнения проверяется по критерию Фишера
![]()
Уравнение значимо, если составлено таким образом F - отношение меньше теоретического: ![]() , где
, где ![]() - число свободы дисперсии адекватности;
- число свободы дисперсии адекватности; ![]() - число степеней свободы дисперсии воспроизводимости; I - число коэффициентов в уравнении регрессии второго порядка, равное числу сочетаний из
- число степеней свободы дисперсии воспроизводимости; I - число коэффициентов в уравнении регрессии второго порядка, равное числу сочетаний из ![]() по 2, т.е.
по 2, т.е.
![]() (20)
(20)
2.3 Рототабельные планы второго порядка
Как было установлено, план второго порядка, представленный в таблице 3, не обладает свойством рототабельности. Рототабельным называют планирование, для которого дисперсия отклика (выходного параметра) ![]() , предсказанного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее неизвестно, где находится та часть поверхности отклика, которая представляет для него особый интерес, поэтому следует стремиться к тому, чтобы количество информации, содержащееся в уравнении регрессии, было одинаково для всех равноотстоящих от центра эксперимента точек. Действительно, удаление от центра точек 5,6,7,8 в
, предсказанного уравнением регрессии, постоянна для всех точек, находящихся на равном расстоянии от центра эксперимента. Экспериментатору заранее неизвестно, где находится та часть поверхности отклика, которая представляет для него особый интерес, поэтому следует стремиться к тому, чтобы количество информации, содержащееся в уравнении регрессии, было одинаково для всех равноотстоящих от центра эксперимента точек. Действительно, удаление от центра точек 5,6,7,8 в ![]() раза меньше, чем удаление точек 1: 2, 3, 4 (см. рисунок 3,: а), и, следовательно, коэффициент уравнения регрессии определяются с различной дисперсией. Бокс и Хантер предложили рототабельные планы 2-го порядка. Для того чтобы композиционный план был рототабельным, величину звездного плеча
раза меньше, чем удаление точек 1: 2, 3, 4 (см. рисунок 3,: а), и, следовательно, коэффициент уравнения регрессии определяются с различной дисперсией. Бокс и Хантер предложили рототабельные планы 2-го порядка. Для того чтобы композиционный план был рототабельным, величину звездного плеча ![]() выбирают из условия:
выбирают из условия:
![]()
![]() (21)
(21)
Или в общем случае
![]() ,
,
где k – число факторов;
p – дробность реплики (для ПФЭ p = 0, для полуреплики p =1, для четвертьреплики p = 2 и т.д.).