Реферат: Математическое моделирование экономических систем 2
Х1 = 200 – 2Х2
(200 – 2Х2 ) + 4Х2 ≤ 300
Х2 = 50
Х1 = 200 – 2·50 = 100.
Подставив в целевую функцию значения Х1 и Х2 , определим максимальную прибыль:
Z (X)max = 5Х1 +6Х2 = 5·100+6·50 = 800 (руб.)
Ответ: Оптимальный выпуск продукции I вида – 100 изделий, II вида – 50 изделий, что позволяет получить максимальную прибыль, равную 800 руб.
Задача 2. Для двух текстильных предприятий (ТП) хлопок закупается случайно n1 раз в течение квартала, при наличии хлопка на одном ТП – n2 раз. Хлопок перерабатывается на одном ТП за q1 часть канала, на двух ТП в 2 раза быстрее. Прибыль для одного работающего ТП составляет π1 , при простое одно ТП терпит убытки в u1 у.е. Определить среднюю прибыль двух ТП в стационарном режиме и в случае уменьшения времени переработки в Rt раз, если прибыль π1 увеличивается в Rπ раз. Принять решение о возможности уменьшения времени переработки.
Дано:
n1 = 2;
n2 = 6;
q1 = 0,12;
π1 = 11;
u1 = 3;
Rt = 1,7;
Rπ = 1.
Решение:
Интенсивность потока заявок, пришедших в систему
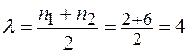 ;
;
Среднее время обслуживания
![]() ;
;
Интенсивность потока обслуживания заявок
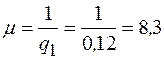 ;
;
Коэффициент загрузки СМО
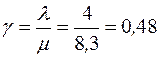 ;
;
Определим вероятности двухканальной СМО:
р0 – оба канала свободны;
р1 – один канал свободен, один канал занят;
р2 – оба канала заняты.