Реферат: Математическое моделирование экономических систем 2

;

.

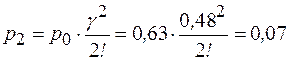Сумма вероятностей равна единице:

.

Определим среднюю прибыль:

,

.

В случае уменьшения времени переработки в R_t раз, если прибыль π₁ увеличивается в R_π раз, получим:

;

;

;

;

.

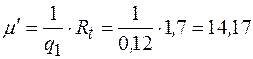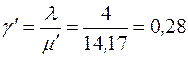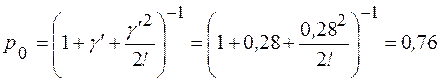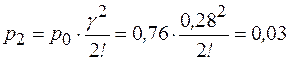Сумма вероятностей равна единице:

.

Рассчитаем новую среднюю прибыль:

,

.

Ответ: В случае уменьшения времени переработки предприятие терпит убытки.

Задача 3. Найдите для получения максимальной прибыли за весь данный период времени управленческие решения о времени замены оборудования стоимостью С у. е., если прибыль от использования оборудования Р и затраты на его ремонт Zизменяются с течением времени Т.

Дано:

С	Р						Z
	Т= 0	Т= 1	Т= 2	Т= 3	Т= 4	Т= 5	Т= 0	Т= 1	Т= 2	Т= 3	Т= 4	Т= 5
10	9	9	9	9	9	9	1	2	4	4	8	9

Решение:

Определяем чистую прибыль от использования оборудования, расчеты сводим в таблицу 1:

π = Р – Z

Таблица 1

Т= 0	1	2	3	4	5
Р	9	9	9	9	9	9
Z	1	2	4	4	8	9
π	8	7	5	5	1	0

Дальнейшие расчеты приведены на рисунке 1.

Ответ: Максимальный эффект использования оборудования составит 20 у. е. при его замене после первого, второго или третьего года службы.

Список использованной литературы

1. Бездудный Ф.Ф., Павлов А.П. Математические методы и модели в планировании текстильной и легкой промышленности: Учебник для вузов. – М.: Легкая индустрия, 1979.

2. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учебное пособие. – М.: Финансы и статистика, 2006.