Реферат: Математическое моделирование экономических систем 2

¦u \¦/ ¦

+-------+ ¦ +-------+ ¦

¦ ИЭ ¦_____________¦\¦/¦__________________¦ УО ¦_____¦______

+-------+ ¦/ \¦ x +-------+ y

К сожалению, многие системы управления формируются по первому способу. Они создают гораздо больше проблем, чем решают. Не высвобождают управленческий персонал и не облегчают его работу, а наоборот - требуют дополнительного персонала и ресурсов. Нужно чтобы ЭВМ состояла при человеке, а не человек при ЭВМ. Но это требует коренной перестройки методов управления, навыков, имеющегося документооборота.

Нужно добиться того, чтобы руководитель получал именно ту информацию, которая ему нужна для принятия решений. Например, директор не должен знать, какие вагоны не поступили, какой груз находится в каждом вагоне, ему нужно знать по каким выпускаемым изделиям имеется недопоставка сырья. Если же директор не соглашается отказаться от лишней информации, значит он в своей деятельности подменяет начальника отдела снабжения, не умеет правильно руководить. ЭВМ берет на себя информационные входы СУ, избавляет от них человека. Часто стараются и ЭВМ избавить от лишней информации - для этого ставят в пунктах сбора данных микро и мини- ЭВМ, которые осуществляют первичную обработку данных перед отправкой в большую ЭВМ.

Практическая часть

Задача 1 . Предприятие производит продукцию двух видов из сырья трех типов. Определить максимум прибыли от реализации с учетом ограничений. Доля сырья первого типа продукции первого и второго вида равны 1 ед. и 2 ед., запасы – 200 ед. Доля сырья второго типа – 1 ед. и 4 ед., запасы – 300 ед. Доля сырья третьего типа – 4 ед. и 1 ед., запасы – 600 ед. Прибыль от единицы продукции первого вида – 5 ед., второго вида – 6 ед.

Решение:

Сведем исходные данные в таблицу:

Тип сырья	Продукция		Запасы, ед.
	I вид	II вид
1	1	2	200
2	1	4	300
3	4	1	600
Прибыль, руб.	5	6	-

Пусть Х₁ и Х₂ – количество изделий I и II вида.

Z (X) = 5Х₁ +6Х₂ → max – целевая функция.

Запишем систему ограничений:

Х₁ +2Х₂ ≤ 200

Х₁ +4Х₂ ≤ 300

4Х₁ +Х₂ ≤ 600

Условие неотрицательности:

Х₁ ≥ 0; Х₂ ≥ 0

(1) Х₁ =0, тогда Х₂ =100;

Х₂ =0, тогда Х₁ =200.

(2) Х₁ =0, тогда Х₂ =75;

Х₂ =0, тогда Х₁ =300.

(3) Х₁ =0, тогда Х₂ =600;

Х₂ =0, тогда Х₁ =150.

По полученным координатам точек строим 3 прямые.

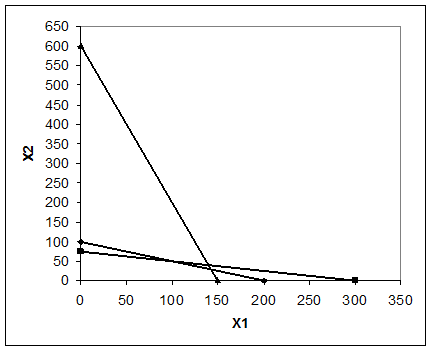
Многоугольник ОАВСD содержит точки, которые являются допустимыми решениями, т.е. удовлетворяют системе ограничений и условию неотрицательности.

Точка С многоугольника ОАВСD является экстремумом функции.

Найдем ее координаты, решив уравнения прямых, на пересечении которых она лежит, т.е. (1) и (2).

Х₁ +2Х₂ ≤ 200