Реферат: Матрицы Метод Гаусса

ПРИМЕР.

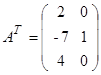
2 3 3 2

ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.

Рассмотрим действия над матрицами.

СЛОЖЕНИЕ МАТРИЦ.

Операция сложения вводится только для матриц одинакового размера.

ОПРЕДЕЛЕНИЕ 7. Суммой двух матриц А = (а _{i j} ) и В = ( b_{i j} ) одинакового размера называется матрица С = (с _{i j} ) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с _{i j =} a _{i j} + b _{i j}

Обозначается сумма матриц А + В.

ПРИМЕР.

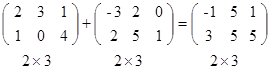
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО

ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k , надо умножить на это число каждый элемент матрицы :

если А= (а _{i j} ), то k · A = (k · a _{i j} )

ПРИМЕР.

СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО

1. Переместительное свойство: А + В = В + А

2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )

3. Распределительное свойство: k · ( A + B ) = k A + k B , где k – число

УМНОЖЕНИЕ МАТРИЦ

Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы В , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.

ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k , элемент которой а _{i j} , расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.