Реферат: Матрицы Метод Гаусса

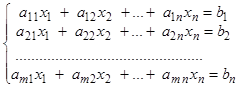
x ₁ , x ₂ , …, x_n – неизвестные.

a_{i j} - коэффициенты при неизвестных.

b_i - свободные члены (или правые части)

Система линейных уравнений называется совместной , если она имеет решение, и несовместной , если она не имеет решения.

Совместная система называется определенной , если она имеет единственное решение и неопределенной , если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными , если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

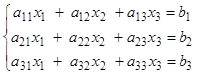( 1 )

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁ . Получим уравнение:

( 2 )

где

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а ₂₁ и а ₃₁ ).

Система примет вид:

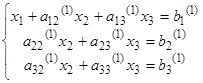( 3 )

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂ из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

( 4 )