Реферат: Матрицы Метод Гаусса
Обозначим: С = А · В.
Если 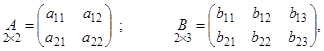 то
то
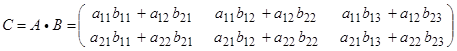
Произведение В ´ А не имеет смысла, т.к. матрицы ![]() не согласованы.
не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А , то, вообще говоря
А ´ В ¹ В ´ А , т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А .
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ . Найти , если можно, А ´ В и В ´ А .
1. 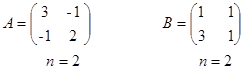
Решение : Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
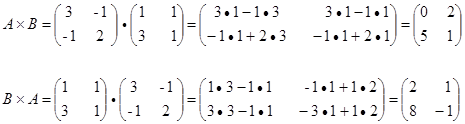
2. 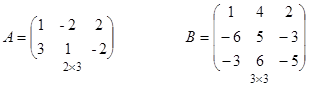
Решение : Матрицы А и В согласованы
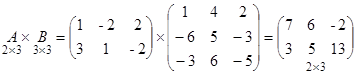
Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель .
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
1. Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
2. Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С ½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль - матрице .
Действие "деление" для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.