Реферат: Механические колебания в дифференциальных уравнениях
Для определения амплитуды и начальной фазы необходимо задать начальные условия. Пусть, например, в начальный момент t = 0 положение груза x=x0 и скорость u=u0 . Тогда 
, откуда
, 
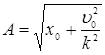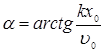
Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных колебаний они зависят от начального состояния системы. При отсутствии начальной скорости (u0 =0) амплитуда А=х0 , а начальная фаза a=p/2 и, таким образом,
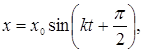или 
Затухающие колебания.
Затухающими колебаниями называются колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшают-ся. Найдем закон движения груза в условиях предыдущей задачи, но с учетом сопротивления воздуха, которое пропорционально скорости движения.
Решение
К силам, действующим на груз, прибавляется здесь сила сопротивления воздуха 
(знак минус показывает, что сила R направлена противоположно скорости u). Тогда дифференциальное уравнение движения в проекции на ось Oxимеет вид
или если положить 
, 
, то
(3)
Это уравнение также является линейным однородным уравнением второго порядка с постоянными коэффициентами. Его характеристическое уравнение:
имеет корни
(4)
Характер движения целиком определяется этими корнями. Возможны три различных случая. Рассмотрим сначала случай, когда 
. Это неравенство имеет место, когда сопротивление среды невелико. Если положить 
, то корни (4) имеют вид 
. Тогда общее решение можно записать в виде
или, преобразовав, умножая и деля на 
, получим:
положим, что
,
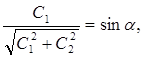
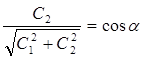тогда
(5)
График зависимости отклонения от положения равновесия от времени имеет вид:
Если заданы начальные условия: 
при t = 0, то можно определить А и a. Для этого находим
и подставляем t = 0 в выражения для 
и 
получим систему уравнений
Разделелив обе части второго уравнения на соответствующие части первого получим