Реферат: Механические колебания в дифференциальных уравнениях

откуда

или а

Так как

то

Решение (5) показывает, что имеют место затухающие колебания. Действии-тельно, амплитуда колебания зависит от времени и является монотонно убывающей функцией, причем при .

Период затухающих колебаний определяется по формуле

Моменты времени, в которые груз получает максимальное отклонение от начала координат (положения равновесия), образуют арифметическую прогрессию с разностью, равной полупериоду Т/2. Амплитуды затухающих колебаний образуют убывающую геометрическую прогрессию со знаменателем, равным или . Эта величина называется декрементом затухания и обычно обозначается буквой D. Натуральный логарифм декремента lnD = - пТ/2 называется логарифмическим декрементом затухания.

Частота колебаний в этом случае меньше, нежели в предыдущем (), но, как и там, не зависит от начального положения груза.

Если сопротивление среды велико и , то, положив , получим корни (4) в виде Так как , то оба корня отрицательны. Общее решение уравнения в этом случае имеет вид

(6)

Отсюда видно, что движение апериодическое и не имеет колебательного характера. Аналогичный характер будет иметь движение и в случае , когда общее решение имеет вид

(7)

Легко заметить, что в обоих последних случаях при имеем .

Если заданы начальные условия и , то в случае, когда , имеем , а . Решая эту систему относительно и , получим

,

и, следовательно

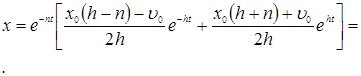
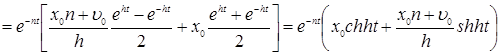
В случае же, когда , получаем , и следовательно,

Вынужденные колебания без учета сопротивления среды.

Вынужденными колебаниями называют колебания, вызванные внешней периодической возмущающей силой.

Пусть груз весом Р подвешен на вертикальной пружине, длина которой в ненагруженном состоянии равна . На груз действует периодическая возмущающая сила где Q и р — постоянные. Найдем закон движения груза, пренебрегая массой пружины и сопротивлением среды.

Решение

Как и для гармонических колебаний, получаем уравнение

Полагая, как и прежде, и, кроме того, перепишем уравнение в виде