Реферат: Механические колебания в дифференциальных уравнениях

,

где М и N — коэффициенты, подлежащие определению. Итак,

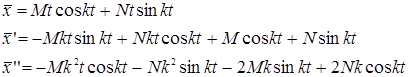
откуда получаем , , и следовательно, частное решение имеет вид

Общее решение в этом случае

(12)

Найдем и подставим в выражения х и значение t=0; получим

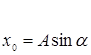
или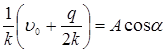

Из последних двух равенств находим

,

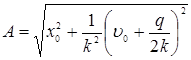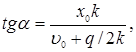
откуда

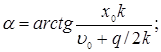
Перепишем общее решение так:

тогда искомое частное решение, удовлетворяющее заданным начальным условиям, запишется в виде.

Выражение (12) показывает, что амплитуда вынужденных колебаний в этом случае может стать неограниченно большой даже тогда, когда q невелико. Иначе говоря, возможно получение сколь угодно больших амплитуд при малых возмущающих силах. Это явление называется резонансом. Таким образом, резонанс наступает тогда, когда частота возмущающей силы совпадает с частотой собственных колебаний.

Впрочем, в действительности точное совпадение этих частот не является необходимым. Выражение (9) для вынужденного колебания показывает, что при близости частот амплитуда может быть очень большой, хотя и ограниченной при фиксированных частотах k и р. Возможностью создания колебаний с значительной амплитудой часто пользуются в различных усилителях, например в радиотехнике. С другой стороны, в большом числе случаев появление больших амплитуд является вредным, ибо может приводить к разрушению конструкций (скажем, мостов или перекрытий).

Вынужденные колебания с учетом сопротивления среды.

Найдем закон движения груза в условиях предыдущей задачи с учетом сопротивления среды, пропорционального скорости движения.

Решение

Как и выше, имеем

или положив, и

(13)

Однородным уравнением, соответствующим (13), является уравнение (3) с корнями характеристического уравнения (4). Предположим, что сопротивление среды невелико, т. е. . При этом общее решение однородного уравнения имеет вид (5):