Реферат: Механические колебания

Составим уравнение плоской гармонической волны, позволяющее определить смещение S точки Б среды, находящейся на любом расстоянии x от начальной точки А, в направлении распространения волны в любой момент времени. Пусть для начальной точки А уравнение колебания: SA = A coswt.

	x

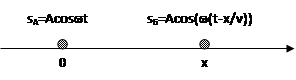Точка Б совершает колебание с запаздыванием по фазе на угол j0 = wt0, соответствующий промежутку времени t, за который волна проходит расстояние x между точками А и Б. Тогда для точки Б уравнение колебания будет:

SБ = A cos(w t - j0) = A cos(w t - w t0) = A cosw (t - t0)

Подставляя значение t0 = , где V - скорость распространения волны, получим:

SБ =. (15)

Заменив в уравнении V = nl и w = 2 pn , тогда:

SБ = .

Таким образом, смещение S точек среды в упругой волне является функцией двух переменных: времени t и расстояния x точки от центра возбуждения колебаний, то есть S = f1(x,t).

Если выбрать определенный момент времени (t1 = const), то уравнение дает зависимость смещения от расстояния x: St = f2(x) , то есть величину смещений точек среды вдоль направления x в заданный момент времени t1. График этой зависимости (как бы моментальный снимок волны) называют графиком волны . Для простой (гармонической) волны график имеет форму синусоиды или косинусоиды.

Зависимость между смещением S точки, ее координатой x и временем t, выраженная в дифференциальной форме называется волновым уравнением.

(16)

Для составления уравнения плоской волны находим частные производные второго порядка от смещения S по времени t и координате x :

(17)

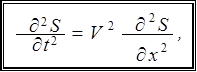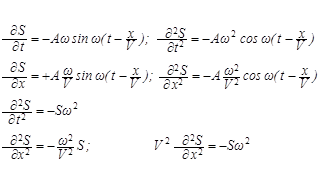
Таким образом, вторая производная смещения по времени пропорциональна второй производной смещения по координате. Коэффициент пропорциональности равен квадрату скорости распространения волны V. Это и есть дифференциальное уравнение плоской волны, распространяющейся в направлении оси xсо скоростью V(см. формулу 17). Оно в наиболее общем виде описывает распространение волнового процесса.

Основные характеристики (амплитуда, период или частота, длина волны и форма колебаний) продольной волны, её уравнение и графику аналогичны поперечной.

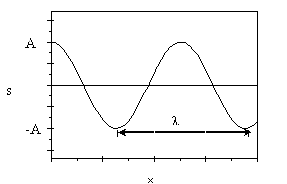
Рис. 7. График плоской волны

1.5 Энергетические характеристики волны

механическое колебание гармонический спектр

При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне не происходит взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения той и другой энергии изменяются одновременно (в фазе) соответственно изменению смещения частиц.

Для мгновенного значения энергии (потенциальной и кинетической) одной частицы можно записать:

, (18)

где S- смещение частицы, w- частота колебания частицы, A- амплитуда колебания частицы, V- скорость волнового процесса, в котором участвует частица, m – масса одной частицы.

Из формулы 18 следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебания, причем в каждый момент времени эти значения для различных частиц отличаются. Однако среднее значение энергии за период колебания для всех частиц одинаково и составляет:

eср = .

Рассчитаем энергию волны для некоторого объема DV среды, в которой она распространяется.

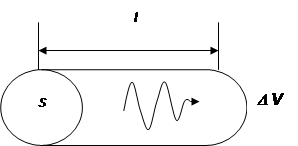Если в единице объема среды содержится N частиц, то r = Nm —плотность среды и среднее значение энергии волны в объеме DV будет:

Е_ср =(19)

где — объемная плотность энергии волны.

Величина, численно равная средней энергии Е_ср , переносимой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность:

Ф = (20)