Реферат: Метод динамічного програмування
1 Принцип оптимальності
Оптимальне керування в будь-який момент часу не залежить від передісторії процесу і визначається тільки станом системи в поточний момент і метою керування. Якщо в якийсь період часу керування було неоптимальним, то наслідки цього в майбутньому виправити вже не можна. Під метою керування розуміються вимоги, яким повинна задовольняти керована система, наприклад, це може бути приведення системи в заданий стан або забезпечення певних умов руху протягом заданого періоду часу.
Отже, принцип оптимальності характеризує наступний за заданим станом рух системи, але він може не мати місця для траєкторії, що передує цьому стану.
2 Метод динамічного програмування
Розглянемо застосування методу динамічного програмування до розв’язання неперервних задач оптимального керування. У цьому випадку треба виконати дискретизацію початкової задачі, тобто початкову задачу потрібно замінити близькою їй дискретною задачею. Розглянемо динамічну систему, закон руху якої описується автономним диференціальним рівнянням
![]() ,(1)
,(1)
де ![]() ,
, ![]() – кусково-неперервні функції.
– кусково-неперервні функції.
Припустимо, що початковий стан системи ![]() заданий, а на керування накладено обмеження
заданий, а на керування накладено обмеження ![]() . Вважатимемо, що час руху
. Вважатимемо, що час руху ![]() фіксований. Цільовий функціонал задачі в цьому випадку матиме вигляд:
фіксований. Цільовий функціонал задачі в цьому випадку матиме вигляд:
![]() .(2)
.(2)
Для дискретизації неперервної задачі (1) – (2) розіб'ємо відрізок ![]() на
на ![]() інтервалів довжиною
інтервалів довжиною
![]()
кожний, де ![]() – натуральне число . Значення функцій
– натуральне число . Значення функцій ![]() і
і ![]() будемо далі визначати лише в дискретні моменти часу
будемо далі визначати лише в дискретні моменти часу ![]() , де
, де ![]() . Для цього введемо позначення
. Для цього введемо позначення ![]() ,
, ![]() , і замінимо диференціальне рівняння (1) різницевим, апроксимуючи першу похідну значеннями в дискретні моменти часу:
, і замінимо диференціальне рівняння (1) різницевим, апроксимуючи першу похідну значеннями в дискретні моменти часу:
![]() .
.
З останнього співвідношення випливає, що
![]() ,
, ![]() .(3)
.(3)
Інтегральному цільовому функціоналу (2) відповідає інтегральна сума
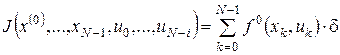 .(4)
.(4)
Отже, ми перейшли до дискретної задачі, у якій потрібно знайти такі керування ![]() , що задовольняють обмеженню
, що задовольняють обмеженню ![]() ,
, ![]() , і мінімізують функціонал (4) за початкових умов
, і мінімізують функціонал (4) за початкових умов ![]() . Очевидно, що результати розв’язання цієї задачі будуть тим точніше апроксимувати початкову неперервну задачу, чим більше
. Очевидно, що результати розв’язання цієї задачі будуть тим точніше апроксимувати початкову неперервну задачу, чим більше ![]() .
.
Розглянемо співвідношення
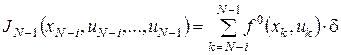 ,
, ![]() ,
,
де ![]() , …,
, …, ![]() визначаються за рекурентними формулами (3), і позначимо
визначаються за рекурентними формулами (3), і позначимо
![]() .
.
Величина ![]() – це частина інтегральної суми (4), що відноситься до моментів часу
– це частина інтегральної суми (4), що відноситься до моментів часу
![]() ,
,
![]()
і залежить від стану ![]() системи в момент часу
системи в момент часу
![]() .
.
Відповідно до принципу оптимальності, керування ![]() на останньому етапі треба обирати так, щоб
на останньому етапі треба обирати так, щоб
![]() .
.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--