Реферат: Метод динамічного програмування

тобто оптимізація процесу проводиться тільки для , тому що для траєкторія вже оптимальна.

Розглянемо поведінку останнього співвідношення при , тобто коли інтервал , на якому шукається оптимальне керування, звужується до точки. Відповідно до закону руху

.

Вважатимемо, що функція Беллмана неперервно диференційована по всіх своїх аргументах. Тоді

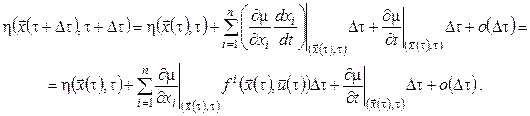(14)

Позначатимемо далі

.

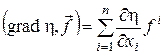Співвідношення (14) з урахуванням цього позначення набуде вигляду

.

Використовуючи останнє співвідношення, рівність (13) можна подати у вигляді

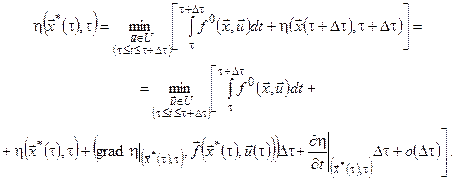(15)

Оскільки функції і 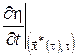у правій частині (15) не залежать від , їх можна винести за знак мінімуму. Після скорочень одержимо

.

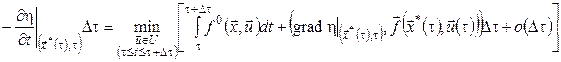Припустимо, що функція є неперервною на відрізку . Розділивши останнє співвідношення на , при одержимо

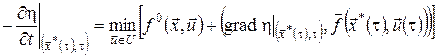.(16)

Останнє співвідношення називається рівнянням Беллмана. Воно є аналогом рекурентних рівнянь Беллмана дискретної задачі оптимального керування для випадку неперервної системи.

Замінивши на , де – оптимальна траєкторія, одержимо з (16)

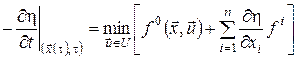.(17)

До рівняння Беллмана додаються крайові умови, що випливають безпосередньо з визначення функції Беллмана:

.(18)

Рівняння Беллмана – це диференціальне рівняння в частинних похідних відносно функції . Але це рівняння не є лінійним через наявність у (17) операції мінімізації. Фактично це означає підстановку в рівняння такого , на якому досягається мінімум і яке змінюється в залежності від значень і .

5 Рівняння Беллмана в задачі з фіксованими кінцями та вільним часом

Додамо до задачі (2), (6), (9) умову закріплення правого кінця траєкторії , де – задано, а – невідомо. У цьому випадку функція Беллмана залежатиме тільки від поточного стану системи. Дійсно, згідно з визначенням функції Беллмана

.

Якщо підінтегральна функція не залежить від , то значення інтеграла при фіксованих і залежить тільки від довжини інтервалу інтегрування , який можна визначити з автономної системи (6), якщо відомі точки і фазової траєкторії. Тому різниця – це функція від аргументів і , а не залежить явно від . У цьому випадку і рівняння Беллмана для задачі із закріпленими кінцями набуває вигляду

.

6 Рівняння Беллмана в задачі швидкодії

Розглянемо задачу оптимальної швидкодії з фіксованими кінцями і вільним часом, закон руху якої має вигляд (6) і задані початковий стан та кінцевий стан . Час невідомий і його потрібно знайти з умови мінімізації цільового функціонала

.