Реферат: Метод динамічного програмування

Доведемо, що спряжені змінні задовольняють спряженій системі

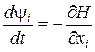, .(21)

Для цього припустимо, що функція Беллмана має неперервні частинні похідні другого порядку. Позначимо

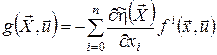.(22)

Оскільки оптимальне керування однозначно визначає оптимальну траєкторію , то функція досягає на кожному фіксованому по змінній максимального значення, рівного 0, у точці , що відповідає оптимальному керуванню в цій точці. У цьому випадку для функції в будь-який момент часу для процесу буде виконана умова

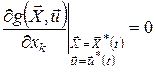, , .(23)

Продиференціюємо співвідношення (22):

, .

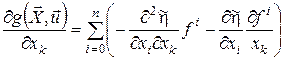Тоді відповідно до (23) для оптимального процесу дістанемо

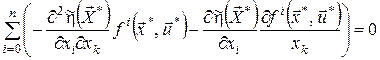, .(24)

Оскільки

,

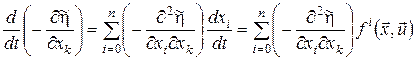то співвідношення (24) можна переписати у вигляді:

,

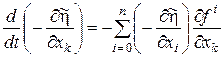або, з урахуванням позначень (21),

, .

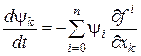Оскільки , то

,

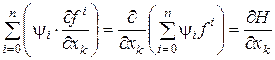а це, у свою чергу означає, що

, .

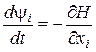Отже, встановлено теоретичний зв'язок принципу максимуму з методом динамічного програмування. Але на практиці виконати подібну операцію не завжди можливо. Так наприклад, рівняння (21) було отримано в припущенні, що функція Беллмана має неперервні похідні другого порядку, що не завжди виконується.

Обидва методи придатні для задач, у яких відсутні обмеження на керування, і всі функції гладкі. Кожний з цих методів може бути застосований там, де не працює інший. Рівняння Беллмана вимагає більше припущень для застосування (неперервність і диференційованість функцій), а принцип максимуму складніше використовувати для розв’язання дискретних задач.