Реферат: Метод динамічного програмування

.

Припустимо, що для будь-якої точки фазового простору і будь-якого моменту часу існує оптимальна траєкторія з початковою умовою , яка надає найменшого значення функціоналу . Позначимо це мінімальне значення через

.

Функція , що задана у всіх точках , простору , , називається функцією Беллмана.

Припустимо, що , , – оптимальний процес і оптимальна траєкторія задовольняє початковій умові . Тоді

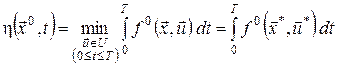
визначає цільовий функціонал (2) початкової задачі.

Розглянемо приріст і відповідний йому момент часу . Очевидно, що останнє співвідношення можна переписати так:

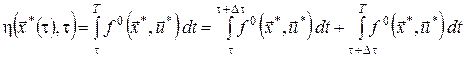.(9)

Відповідно до принципу оптимальності, відрізок оптимальної траєкторії від точки до точки також є оптимальною траєкторією, тобто

,

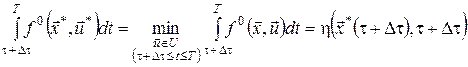тому співвідношення (9) можна переписати у вигляді

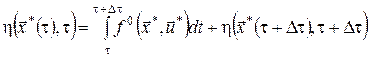.(10)

Очевидно, що другий доданок в (10) залежить від стану системи (оскільки оптимальне значення функціонала залежить від початкового стану системи і для кожного початкового стану оптимальне значення функціонала різне). У цей стан , у свою чергу, система попадає під дією керування , яке діє на інтервалі часу . Отже, значення залежатиме від вибору керування на відрізку .

Дійсно, розглянемо різні припустимі керування на відрізку . Їм відповідатиме набір траєкторій , що виходять із точки , яка лежить на оптимальній траєкторії . На кожній траєкторії із цього набору фазова точка в момент часу попаде в деякий стан .

Виберемо керування на відрізку так, щоб траєкторія на цьому відрізку була оптимальною. Це оптимальне керування в загальному випадку різне для кожної траєкторії пучка. Очевидно, що вибираючи одне – оптимальне – серед всіх можливих керувань , для кожної із траєкторій , ми фіксуємо подальший стан кожної із них і при цьому одержуємо мінімальне значення функціонала

,

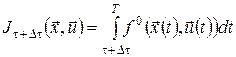яке дорівнює

.

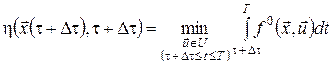Очевидно, що це значення залежить від стану . А оскільки, як було встановлено раніше, стан залежав від вибору керування на відрізку , то й значення також залежатиме від того, яким було обрано керування , .

Розглянемо значення функціонала на траєкторіях з набору, побудованого вище при . Оскільки відрізок кожної траєкторії від точки до точки є оптимальним відповідно до принципу максимуму, то значення функціонала дорівнює

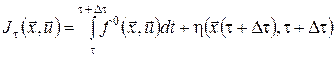.(11)

Ясно, що останнє співвідношення різне для кожної з траєкторій і відповідного цій траєкторії керування на відрізку . Виберемо серед всіх значень мінімальне. Оскільки обидва доданки в (11) залежать тільки від вибору керування на інтервалі , то і мінімальне значення (11) залежатиме тільки від вибору керування на цьому інтервалі, тобто

.

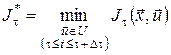Побудований набір траєкторій є підмножиною більш широкої множини всіх припустимих функцій, на яких шукається найменше значення функціонала . Тому в загальному випадку має місце нерівність

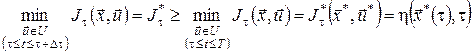.(12)

Але оскільки оптимальна траєкторія належить до побудованого набору траєкторій, то в співвідношенні (12) насправді має місце рівність, тобто

.

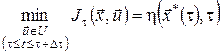Звідси з урахуванням (11) одержимо