Реферат: Методы и анализ нелинейного режима работы системы ЧАП. Метод фазовой плоскости

Eсли в системе возникают периодические колебания, на фазовой плоскости они отображаются в виде замкнутой кривой, называемой предельным циклом. Предельный цикл является устойчивым, если при некоторых отклонениях от него фазовая траектория вновь стремится к предельному циклу. При расхождении фазовых траекторий предельный цикл называется неустойчивым.

Построение фазовых траекторий позволяет судить о свойствах нелинейных систем по переходному процессу.

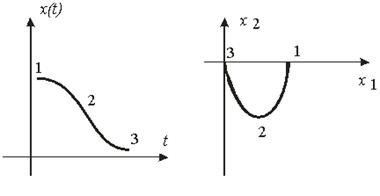
Рис.7. Апериодический процесс и его фазовая траектория.

Построение фазового портрета системы обычно начинают с определения его характера вблизи точек равновесия системы, в которых производные . Координаты точек равновесия определяются, как следует из (8), равенствами , . Точки равновесия при построении фазового портрета системы называют особыми.

Поведение фазовых траекторий вблизи особых точек зависит от характера корней соответствующего характеристического уравнения

,

где

, ;

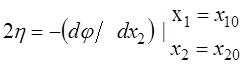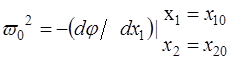- отклонение от состояния равновесия.

Если и , то процесс является затухающим гармоническим колебанием

, (10)

где и - амплитуда и начальная фаза колебания; - его частота, равная

.

Продифференцировав выражение (10) для по времени, получим

. (11)

Фазовая траектория, построенная по приведённым выражениям для процессов и , имеет вид скручивающейся спирали (см. рис.8), получившей название – устойчивый фокус.

При и процесс является гармоническим колебанием с нарастающей амплитудой. Особая точка соответствует при этом неустойчивому состоянию равновесия и называется неустойчивым фокусом (см. рис.9).

При выполнении условия корни действительные и имеют одинаковый знак. Если они отрицательны, то особая точка является устойчивым узлом (см. рис.10). Положительным корням соответствует особая точка типа неустойчивого узла (см. рис.11). При корни действительные и имеют разные знаки. Особая точка называется седлом (см. рис.12).

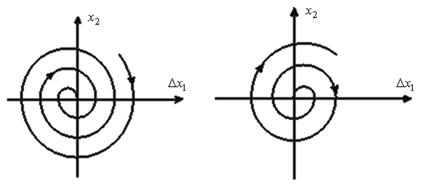
Рис.8. Устойчивый фокус.

Рис.9. Неустойчивый фокус.

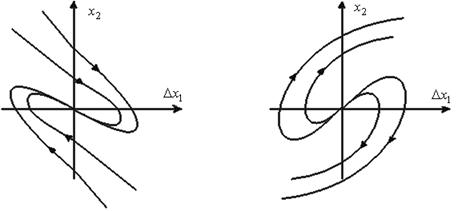
Рис.10. Устойчивый узел.

Рис.11. Неустойчивый фокус

.

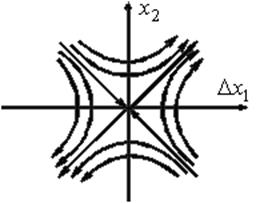
Рис.12. Особая точка типа седла.

Для построения фазового портрета необходимо определить изоклины. Изоклиной называют геометрическое место точек в котором касательные к фазовым траекториям имеют постоянный наклон.