Реферат: Методы и анализ нелинейного режима работы системы ЧАП. Метод фазовой плоскости

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра РТС

РЕФЕРАТ

На тему:

" Методы и анализ нелинейного режима работы системы ЧАП. Метод фазовой плоскости"

МИНСК, 2008

К нелинейным относят системы, описываемые нелинейными дифференциальными уравнениями.

Система является нелинейной вследствие наличия в ее составе звеньев, описываемых нелинейными дифференциальными уравнениями, или имеющих нелинейную статическую характеристику (например, дискриминационную).

Нелинейный режим работы имеет место в системе при выходе ошибки слежения за пределы линейного участка (переходной режим, срыв слежения, большой уровень помех и т.д.).

Методы анализа нелинейных систем:

Метод кусочно-линейной аппроксимации. Нелинейная характеристика разбивается на ряд линейных участков, в пределах каждого из которых система описывается линейным дифференциальным уравнением. Далее на каждом из этих участков система исследуется линейными методами; находятся решения, описывающие работу системы, которые затем "сшиваются". Метод удобен при небольшом числе участков разбиения. Недостаток метода в громоздкости вычислений при увеличении количества участков.

Метод гармонической линеаризации. Нелинейный элемент (НЭ) заменяется его линейным эквивалентом. Критерий эквивалентности состоит в равенстве первой гармоники напряжения на выходе НЭ и его линейного эквивалента по амплитуде и фазе при подаче на входы НЭ и его эквивалента гармонического сигнала. Метод эффективен, когда все высшие гармоники подавляются последующими цепями.

Метод фазовой плоскости. Применяется для исследования нелинейных систем, описываемых дифференциальными уравнениями первого и второго порядков. Состоит в построении и исследовании фазового портрета системы в координатах исследуемой величины и ее производной.

Используется для анализа переходных режимов работы, оценки устойчивости системы, возможности возникновения периодических колебаний.

Моделирование на аналоговых и цифровых вычислительных машинах. Не имеет ограничений на количество и вид нелинейностей, порядок дифференциального уравнения, позволяет исследовать поведение системы при детерминированных и случайных воздействиях.

Отсутствие возможностей найти аналитические зависимости для исследуемых явлений является недостатком метода.

Метод статистической линеаризации. Состоит в замене НЭ его статистическим линейным эквивалентом. Используется для исследования нелинейных систем, описываемых дифференциальными уравнениями произвольного порядка. Метод является приближенным. Имеет место неоднозначность в решениях при использовании различных критериев эквивалентности замены.

Метод, основанный на использовании марковской теории случайных процессов позволяет исследовать системы, описываемые дифференциальными уравнениями первого и второго порядков, работающие в условиях действия случайных возмущений, и получить аналитические выражения для этих систем, что является его достоинством.

На практике используют комбинацию различных методов.

Анализ нелинейного режима работы системы ЧАП

Для определения некоторых характеристик системы, произведем качественный анализ системы ЧАП (рис.1)

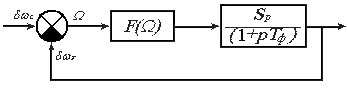
Рис.1. Структурная схема нелинейной системы.

Исходные данные:

─ крутизна регулировочной характеристики генератора;

─ дискриминационная характеристика;

─ нестабильность частоты генератора;

─ флюктуационная составляющая;

─ отклонение от частоты от номинального значения. .

--> ЧИТАТЬ ПОЛНОСТЬЮ <--