Реферат: Методы оценки температурного состояния

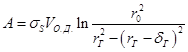,(2.15)

где и - радиус заготовки до прошивки и радиус гильзы; - толщина стенки гильзы; - сопротивление металла деформированию, рассчитывается по эмпирической формуле

,(2.16)

- сопротивление деформации, выбираемое по величине среднего единичного обжатия; - обжатие в пережиме.

Теплота, поступающая в металл при трении, рассчитывается по формуле:

,(2.17)

в которой - коэффициент, учитывающий долю теплоты, поступающей на оправку от трения; - плотность теплового потока за счет работы сил трения; - коэффициент контакта; - площадь поверхности металла под оправкой; - время прошивки.

Тепловые потери металла в очаге деформации за время прошивки составляют величину:

,(2.18)

где , и - площади поверхностей контакта металла с валками, линейками и окружающей средой; , , , - плотности тепловых потоков; - плотность потока тепловых потерь в окружающую среду; и - плотности потоков тепловых потерь к валкам и линейкам рассчитываются при допущении квазистационарного режима теплопроводности с учетом температурного сопротивления слоя окалины:

,(2.19)

где и - температура валков и линеек в стационарном режиме работы.

Кондуктивный теплообмен между металлом и оправкой через слой окалины в месте контакта или через воздушный зазор, в первом приближении, рассчитывается при допущении квазистационарного режима теплообмена.

Через слой окалины:

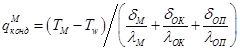; (2.20)

через воздушный зазор:

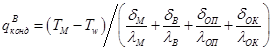,(2.21)

где - средняя температура металла при прошивке; - температура поверхности оправки; , - толщина приграничного слоя металла и оправки; , - толщина окалины и воздушной прослойки; , , , - коэффициенты теплопроводности деформируемого металла, оправки, окалины и воздуха соответственно.

Плотность лучистого теплового потока в воздушном зазоре находится при допущении равенства поверхностей, расположенных по обе стороны зазора. Учитывая, что воздух является диатермичной средой, получим

,(2.22)

где - постоянная Стефана - Больцмана; - приведенная степень черноты. Плотность теплового потока, выделяемого при работе сил трения, определяется по формуле:

,(2.23)

где - касательное напряжение трения; - скорость перемещения металла вдоль оси оправки (оси Oz).

Касательное напряжение трения рассчитывается по формуле

,(2.24)

в которой - коэффициент трения; Р - сила нормального давления на оправку.

Для конических оправок различных геометрических размеров значения давлений, сохраняются на носке, в конце сферической части, в пережиме и в конце третьего участка.

Скорость течения металла в рассматриваемом расчетном сечении находится из уравнения неразрывности, которое при некотором допущении имеет вид:

,(2.25)