Реферат: Минимизация функций алгебры логики

0-Группа: 0---

Запишем таблицу исходных min-термов, где функция равна 1:

0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1011	1111
V	V	V	V	V	V	V	V	0---

Выделим минимальное число групп, покрывающих

Для проверки составим таблицу истинности

1000	1001	1011	1111
-00-	V	V
-0-1	V	V
-111	V	V

Метод минимизирующих карт (для ДСНФ и КСНФ). (1.5)

Одним из способов графического представления булевых функций от небольшого числа переменных являются карты Карно. Их разновидность – карты Вейча, которые строятся как развертки кубов на плоскости, при этом вершины куба представляются клетками карты, координаты которых совпадают с координатами соответствующих вершин куба.

Для ДСНФ единицы ставятся в клетке, соответствующей номеру набора, на котором значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот.

Диаграмма для двух логических переменных (для ДСНФ):

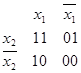
Для трех переменных:

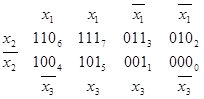
Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие на границе карты.

При числе переменных 5 и больше отобразить графически функцию в виде единой плоской карты невозможно. Тогда строят комбинированные карты, состоящие из совокупности более простых карт. Процедура минимизации заключается тогда в том, что сначала находится минимальная форма 4-х мерных кубов (карт), а затем, расширяя понятие соседних клеток, отыскивают min-термы для совокупности карт. Причем соседними клетками являются клетки, совпадающие при совмещении карт поворотом вокруг общего ребра.

Пример: Минимизировать ФАЛ от двух переменных:

	1	1
	1

Минимизировать функцию:

	1	1	1
	1

Минимизация логических функций, заданных в базисе .

Метод неопределенных коэфициентов применим для минимизации функций, заданных в различных базисах. Пусть функция является ПСНФ, операция имеет особенности, отличающие ее от операции дизъюнкции.

1)

2)

3)

Минимизация при этом усложняется, так как ее основными критериями являются минимальные ранги каждого терма и их минимальное количество, при этом в ходе минимизации в базисе нецелесообразно приравнивать к нулю все коэффициенты на наборах где , т.к. в наборах, где функция могут остаться термы высокого ранга. Поэтому особой разницы между выбором нулевого или единичного значения функции нет.

Количество коэффициентов, остающихся в нулевых строках должно быть четным, а в единичных – нечетным. Лучше всего рассматривать единичные строки и оставлять те коэффициенты минимального ранга, которые чаще всего повторяются в этих строках. В общем случае для получения минимальной формы выполняют следующие действия:

1) Подсчитывают, сколько раз в единичных строках встречаются термы первого ранга и оставляют из них те, которые встречаются максимальное число раз.

2) Находят нулевые строки, в которых встречаются оставленные в первом шаге термы и их не обнуляют.

3) Рассматривая нулевую строку, в которой остался одни единичные термы и находят в ней еще единичный терм, встречающийся максимальное число раз в единичных строках, в которых еще не было оставлено ни одного терма и.т.д.

Метод Квайна-Мак-Класки может быть применим при минимизации этого базиса, при этом кроме эффективных значений функции, где включаются некоторые min-термы, где . Метод Квайна-Мак-Класки применим для минимизации базисов стрелки пирса и штриха Шеффера.

Не полностью определенные ФАЛ (1.6)