Реферат: Минимизация функций алгебры логики

Определение : Производной первого порядка от булевой функции по переменной называется выражение:

Где первая - единичная остаточная функция, а вторая- нулевая остаточная функция.

Пример:

после минимизации получим:

производная первого порядка по переменной определяет условие, при котором эта функция изменяет свое значение при перемене значения с 0 на 1.

Для данной функции получим схему:

---

Смешанные производные k-го порядка.

Определение : смешанной производной k-го порядка называется выражение вида:

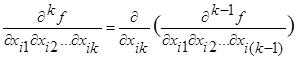
При этом порядок фиксированной переменной не имеет значения. Производная k-го порядка 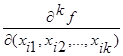определяет условия, при которых эта функция изменяет свое значение при одновременном изменении значений .

Согласно Бохману, производная k-го порядка вычисляется по формуле:

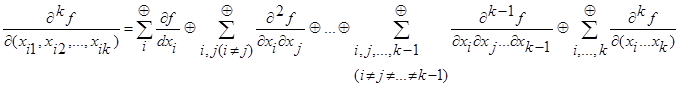Пример: определить условия переключения выходного канала функции при переключении каждого канала, первого и второго канала, всех каналов одновременно.

1)

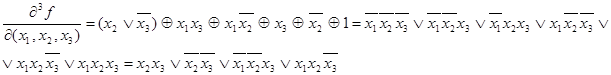
Понятие производной от булевых функций используется для синтеза логических схем, а также в теории надежности.

Приложение алгебры логики. (1.8)

1) Для решения логических задач, - суть в том, что имея конкретные условия логической задачи стараются записать их в виде ФАЛ, которые затем минимизируют. Простейший вид формуды, как правило, приводят к ответу на задачу.

Задача: