Реферат: Модели систем массового обслуживания. Классификация систем массового обслуживания
и решение матричного уравнения сводится к решению системы трёх уравнений:
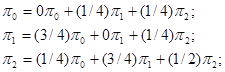
Коэффициенты первого уравнения в этой системе дополняют до единицы сумму коэффициентов второго и третьего уравнений; это свидетельствует о линейной зависимости между ними. Поэтому для решения системы уравнений нужно ввести дополнительное нормирующее условие. В данном примере: ![]() .
.
Решая систему полученных уравнений, имеем:
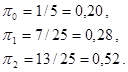
Уравнение для вероятности достижения состояния в переходном режиме решить значительно труднее. Некоторого упрощения можно достигнуть, используя z – преобразование. Применим его к уравнению для переходных вероятностей
![]() .
.
Обозначая соответствующие преобразования, получим: ![]()
Все полученные здесь математические результаты относились к однородным Марковским процессам, где вероятности переходов не зависят от времени. В более общем случае такая зависимость имеет место.
Рассмотрим вероятности перехода системы из состояния i на m-том шаге в состояние j на n-том шаге для n > m.
Можно показать, что эти вероятности связаны между собой, так называемым уравнениями Чепмена-Колмогорова.(Chapman - Kolmogorov)
![]() .
.
Для однородных цепей Маркова эти уравнения упрощаются так как
![]() .
.
И сводятся к анализируемым выше.
Непрерывные цепи Маркова.
Случайный процесс X(t) с дискретным множеством значений образует непрерывную цепь Маркова, если
![]() .
.
Будущие состояния зависят от прошлого только через текущее состояние. Для непрерывный цепей Маркова основным также является уравнение Чепмена –Колмогорова, для однородной цепи имеющее вид: ![]() .
.
Здесь матрица H (t)= [ pij (t)] - матрица вероятностей перехода из состояния i в состояние j в момент времени t , а матрица Q называется матрицей интенсивностей переходов. Ее элементы имеют следующий смысл: если в момент времени t система находилась в состоянии Ei , то вероятность перехода в течение промежутка времени (t,t+Δt) в произвольное состояние Ej задается величиной qij (t)Δt + o(Δt), а вероятность ухода из состояния Ei величиной -qii Δt + o(Δt).
Таким образом, интенсивности переходов можно вычислять как соответствующие пределы при стремлении к нулю длительности временного интервала.
Наиболее важным для дальнейшего использования является класс непрерывных цепей Маркова называемых «процессами гибели - размножения» ( Birth – deathprocess). Для таких систем из состояния k возможны переходы только в состояния k, k-1 и k+1 в следующие моменты времени:
· в момент t объем популяции был равен k и в течение времени (t,t+Δt) не произошло изменения состояния
· в момент t объем популяции был равен k-1 и в течение времени (t,t+Δt) родился один член популяции
· в момент времени t объем популяции был равен k+1 и в течение времени (t,t+Δt) погиб один член популяции
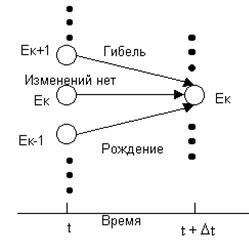
Рис. 1. Возможные переходы в состояние Ек.
Будем искать вероятность того, что в момент времени t объем популяции равен k , обозначив его Pk (t). Можно записать соотношения для вероятности достижения состояния k в момент времени t+Δt:
![]() .
.