Реферат: Модели систем массового обслуживания. Классификация систем массового обслуживания

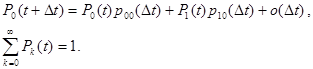
Выразим вероятности переходов за интервал Δt через интенсивности

Вер(+1)=λ_k Δt+o(Δt) ; Вер(-1)=μ_k Δt+o(Δt).

Вероятность нуля рождений 1- λ_k Δt+o(Δt) , а нуля гибелей 1- μ_k Δt+o(Δt).

Таким образом, вероятность того, что состояние k сохранится неизменным, будет равно произведению [1- λ_k Δt+o(Δt)][ 1- μ_k Δt+o(Δt)].

Тогда уравнения Чепмена-Колмогорова приобретают вид

Раскрывая скобки и проводя деление на Δt, получим:

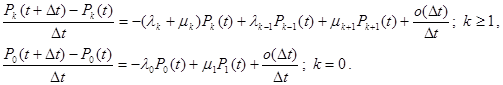
В пределе получается система дифференциально-разностных уравнений, решение которой будут играть важную роль для практических задач.

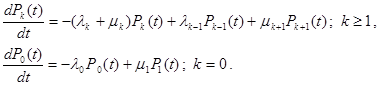
В соответствие этой системе уравнений можно поставить наглядную диаграмму интенсивностей переходов, которая аналогична диаграмме переходов для дискретных цепей Маркова (Рис. 2)

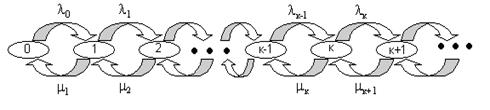
Рис. 2 Диаграмма интенсивностей переходов для процесса размножения и гибели.

Овалам здесь соответствуют дискретные состояния, а стрелки определяют интенсивности потоков вероятности (а не вероятности !) переходов от одного состояния к другому.

Имеет место своеобразный «закон сохранения »:

Разность между суммой интенсивностей, с которой система попадает в состояние k и суммой интенсивностей, с которой система покидает это состояние должна равняться интенсивности изменения потока в это состояние (производной по времени).

Применение закона сохранения позволяет получать уравнения для любой подсистемы Марковской цепи типа процесса «гибели-размножения». Особенно эффективным оказывается построение решений в стационарном, установившемся режиме, когда можно полагать что вероятности в произвольный, достаточно отдаленный момент времени, остаются постоянными.

Приравнивая производную по времени нулю, получаем систему разностных уравнений

Полагая, что интенсивности λ_-1 =λ_-2 = λ_-3 =…0; μ₀ = μ_-1 = μ_-2 = μ_-3 =…=0, второе уравнение выписывать отдельно далее не потребуется. Итак, стационарный режим в цепи Маркова будет описываться системой разностных уравнений и условием нормировки для вероятностей

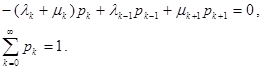
Нетрудно видеть, что эти уравнения легко выводятся из закона сохранения интенсивностей вероятностей. В стационарном режиме разность потоков равна нулю и полученные выше уравнения приобретают смысл уравнений равновесия или баланса, как их и называют.

.

Интенсивность потока вероятностей в состояние k равна интенсивности потока из этого состояния.

Решать уравнение баланса можно, сначала определив при k =0 значение

.

Затем, построив систему уравнений для k =1, можно получить .

Далее получаем