Реферат: Надёжность технических систем
математическое ожидание случайной величины T
,
дисперсия случайной величины T
.
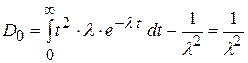Экспоненциальный закон в теории надёжности нашел широкое применение, так как он прост для практического использования. Почти все задачи, решаемые в теории надёжности, при использовании экспоненциального закона оказываются намного проще, чем при использовании других законов распределения. Основная причина такого упрощения состоит в том, что при экспоненциальном законе вероятность безотказной работы зависит только от длительности интервала и не зависит от времени предшествующей работы.
Экспоненциальное распределение широко применяется для оценки надежности энергетических объектов.
Графики изменения показателей надёжности при экспоненциальном распределении приведены на рис.2.7 .
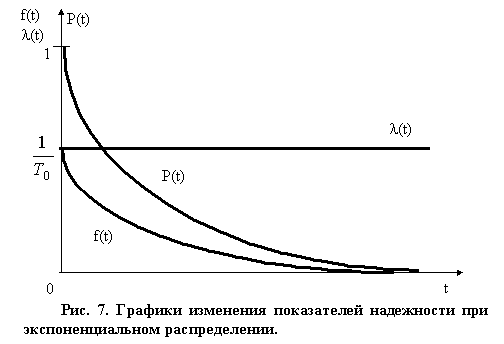
Рис. 2.7.
Нормальное распределение
Нормальное распределение является наиболее универсальным, удобным и широко применяемым. Считается, что наработка объекта подчинена нормальному распределению (нормально распределена), если ПРО описывается выражением:
,
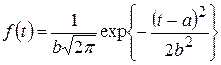где a и b - параметры распределения, соответственно, МО и СКО, которые по результатам испытаний принимаются: 
, где 
и 
- оценки средней наработки до отказа и дисперсии ( 
- СКО).
Т.о. ПРО имеет вид
. ( 
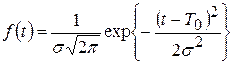- МО наработки).
Колоколообразная кривая плотности распределения приведена на рис. 2.8.
Интегральная функция распределения имеет вид
.
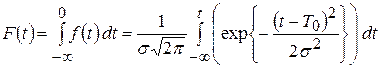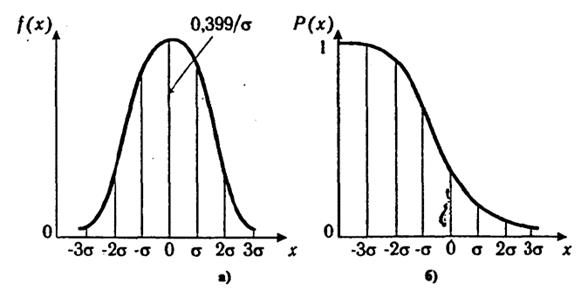
Рис. 2.8 Кривые плотности вероятности (а) и
функции надежности (б) нормального распределения
Вычисление интегралов заменяют использованием таблиц нормального распределения, при котором 
= 0 и s = 1. Для этого распределения функция плотности распределения отказов имеет одну переменную t и выражается зависимостью
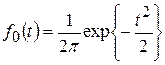
Величина t является центрированной (так как = 0) и нормированной (так как σt = 1).
Функция распределения соответственно запишется в виде:
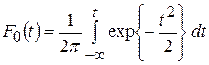
Значение функции распределения определяется формулой
F ( t ) = 0,5 + Ф( u ) = Q ( t ) ;
где Ф – функция Лапласа, u = (t - T 0 )/s - квантиль нормированного нормального распределения. Т.е. функция распределения представляет собой ВО.
При использовании функции Лапласа вместо интегральной функции распределения F 0 (t ) имеем
,
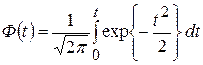ВО и ВБР, выраженные через функцию Лапласа, имеют вид
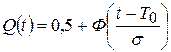, (Ф от (и ), а не умножить!!!)
.
Вероятность попадания случайной величины Х в заданный интервал значений от α до β вычисляют по формуле
.
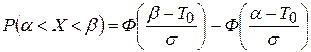Значения функции Лапласа Ф и u – табулированы.
Общий характер изменения показателей надёжности при нормальном распределении приведён на рис. 2.9 .
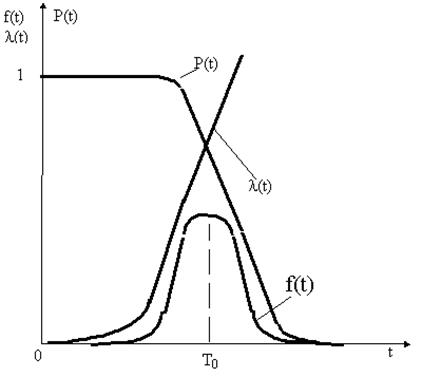
Рис. 2.9.
Нормальный закон распределения часто называют законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения.
Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную и далее плотность снижается.
Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы.
2.2.3 Расчёт характеристик надёжности невосстанавливаемых объектов при основном соединении элементов