Реферат: Некоторые главы мат. анализа

и вообще

.

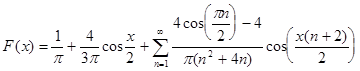Найдем первые пять гармоник для найденного ряда:

1-ая гармоника

2-ая гармоника

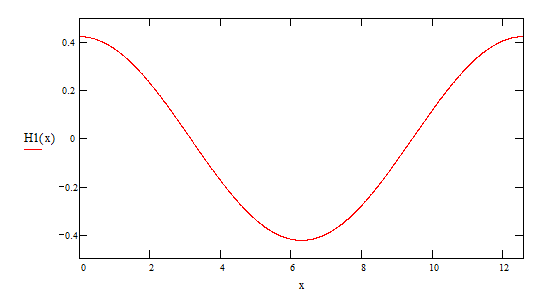
3-я гармоника

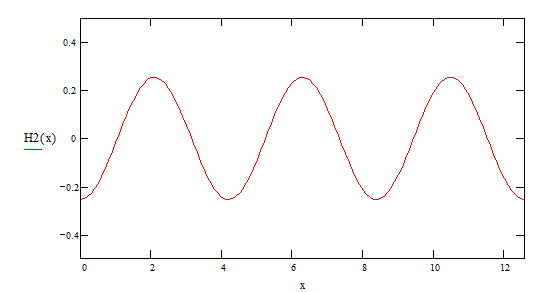
4-ая гармоника

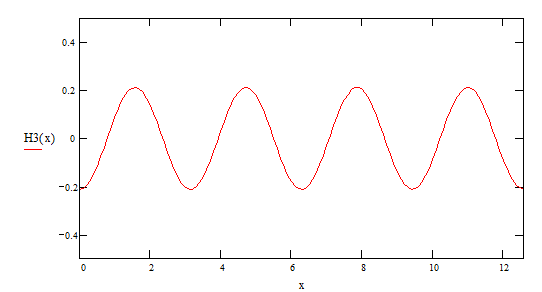
5-ая гармоника

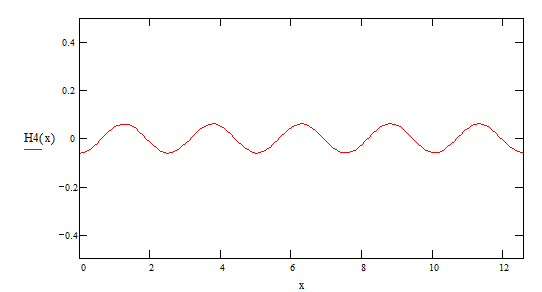
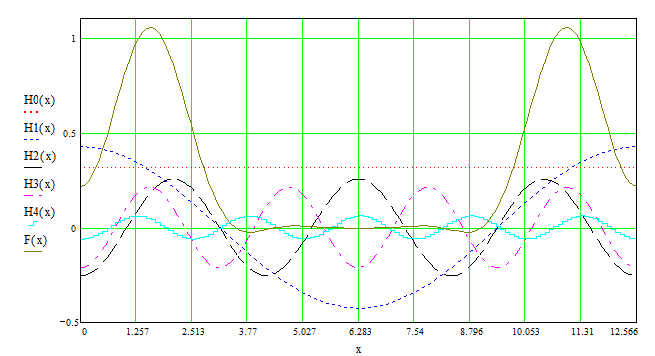
А теперь рассмотрим сумму этих гармоник F(x):

Комплексная форма ряда по косинусам

Для рассматриваемого ряда получаем коэффициенты (см. гл.1)

,

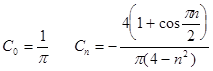но при не существует, поэтому рассмотрим случай когда n =+2 :

(т.к. см. разложение выше)

и случай когда n =-2:

( т.к. )

И вообще комплексная форма:

или

или

Разложение нечетной функции в ряд

Аналогичным образом поступаем с данной функцией F(x), продлевая ее как нечетную, и рассматриваем на промежутке от 0 до смотри рис.3

Рис.3

поэтому разложение по синусам имеет вид:

Из данного разложения видно, что при n =2 произведение неопределенно (можно не учесть часть суммы), поэтому рассмотрим два отдельных случая.